球面調和関数とCG. Part1, ~Light Probeは何を計算しているのか?~
はじめに
3DCGをやっている方だとSpherical Harmonics(SH)、日本語で球面調和関数というのをちらほら耳にするかと思います。UnityやUEにおけるLight ProbeではSHが使われており、業務でも触ったことがある方は多いのではないでしょうか。
その普及率の反面、SHそのものについての情報は世間的に少ないように感じます(特に日本語)。
私も、使い方はわかっても、一体これはどういう原理で計算しているのか、事前計算で求めている係数たちは何を表しているのかは正直よくわかっていませんでした。
ということで、SHについて調べてみました。この記事は特にLight Probeの解明を目的にSHの解説をしていこうと思います。
この記事では以下の知識を前提としています。
- 基本的な3DCGの照明計算
- 大学1~2年生程度の数学(主に微分積分)
また、座標系についてはZ-upの右手座標系を前提に議論を進めます。
Spherical Harmonicsとは
Spherical Harmonics(SH)は、3次元単位球面$S^2$上で定義される特に性質の良い関数たち $Y_\ell^m$ のことを言います。具体的な式や性質などの詳細は後ほど説明します。
単位球面上で定義されるというのは、球面 $S^2$の点$(x,y,z)$ があった時それを引数として何らかの値を返す関数 $Y_\ell^m(x,y,z)$ という意味です。馴染みがなければピンとこないかもしれませんが、これは平たく言えば方向を引数に取る関数です。
方向ベクトル $\omega = (x,y,z)$ はノルムが $\sqrt{x^2 + y^2 + z^2} = 1$ であり、ちょうど単位球面 $S^2$ 上の点と1対1の関係を持ちます。
数学的な文脈では度々、方向ベクトル全体の集合を $S^2$ と表現することがあります。なので、SHはシンプルに方向ベクトル $\omega$ を引数に取る関数 $Y_\ell^m(\omega)$ として書くことができます。
方向はいわゆる直交座標 $(x,y,z)$ で表示してもよいのですが、極座標における角度 $(\theta, \phi)$ でも表示することができます(球面座標)。ここでは、$\theta$ のことを極角(Polar Angle)、$\phi$ を方位角(Azimuthal Angle)と呼称します。
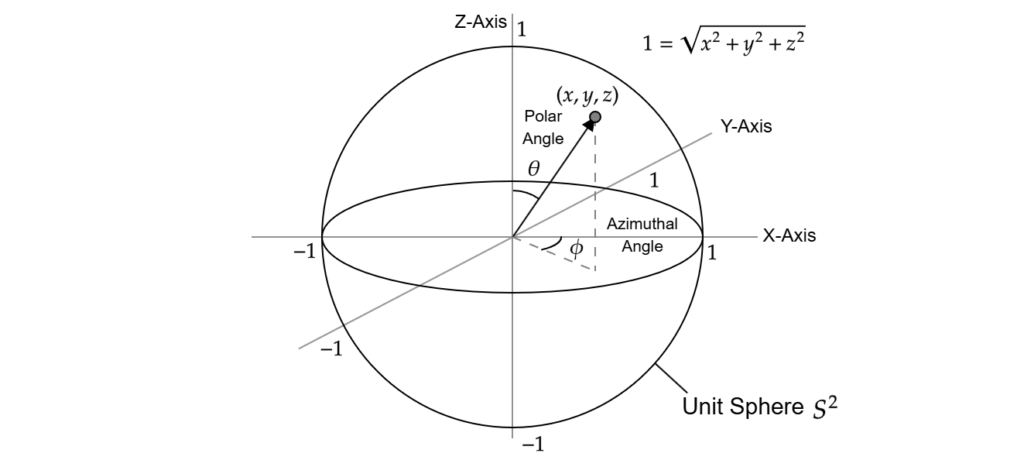
今回の記事ではこれら3つによる $Y_\ell^m(\omega)$, $Y_\ell^m(x,y,z)$, $ Y_\ell^m(\theta,\phi)$ という表記を使用しますが、どれも同じことを表していることに留意してください(都度、使いやすいものを使用します)。また、簡略のため引数を省略した $Y_\ell^m$ という表記を使用することがあります。
複素関数と実関数
SHには大きく分けて複素数を返す複素関数と実数を返す実関数の2つのバージョンがあります。今回の記事ではこれらを区別するため、複素関数を $Y_\ell^m$ として、実関数は添え字を並べた $Y_{\ell,m}$ と表記し、それぞれを特に複素SH、実SHと呼称することにします。
- 複素SH $Y_\ell^m : S^2 \rightarrow \mathbb{C}$
- 実SH $Y_{\ell,m} : S^2 \rightarrow \mathbb{R}$
次数と位数
SHは一つだけではなく、無限に存在しており、それらは次数 $\ell$ と位数 $m$ の二つのIndexによって指定されます。例えばですが、$Y_1^1$, $Y_4^2$ といったような形です。
次数 $\ell$ は自然数 $\ell = 0, 1, 2, 3, …$ の範囲を取るindexで、役割としてはSHの全体的な性質を決定するものです。同じ次数を持つSH同士は近い性質を持ち、対照的に次数が異なれば大きく形が変わります。
位数 $m$ はそんな次数 $\ell$ に依存したindexで、$|m| \le \ell$ を満たす整数に限られます。例えば $\ell = 0$ であれば $m = 0$、$\ell = 1$ なら $m = -1, 0, 1$、$\ell = 2$なら $ m = -2, -1, 0, 1, 2$ となります。役割としては $\ell$ に対するバリエーションを持たせるもので、似たような性質を持つSHを作り出します。
例として実SHを球面上にプロットした図が以下になります。黄色になるほど高く、藍色になるほど小さい値を示します。$\ell =0$ は例外的に定数ですが、それ以外は指向性を持ち、各々は特有の方向に対して強い値を持つような関数であることが見て取れます。
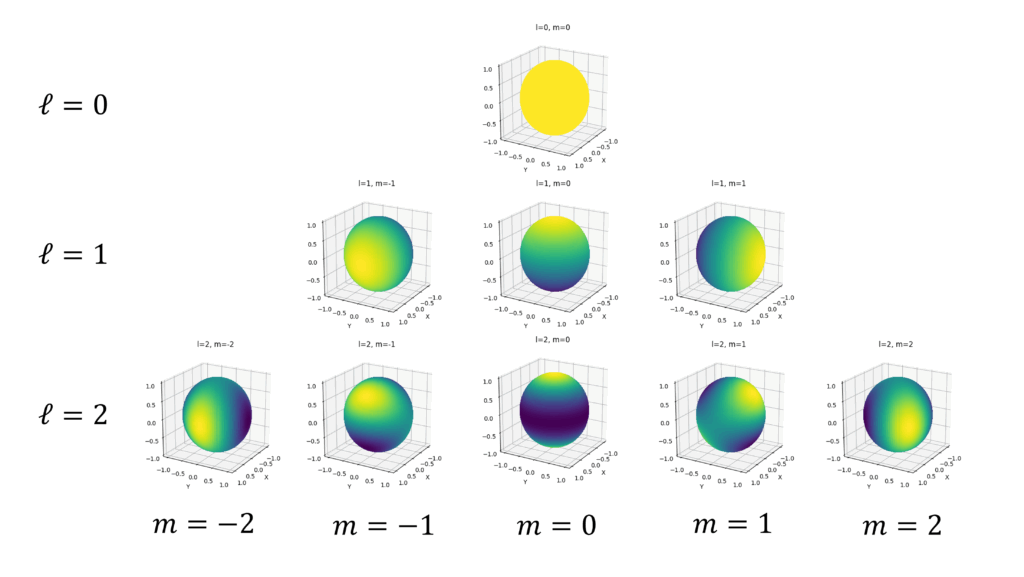
これだと裏側が分かりづらいので、世界地図のように球面を展開して、縦軸を $\theta$、横軸を $\phi$ とする2次元のプロットを次のように示します。
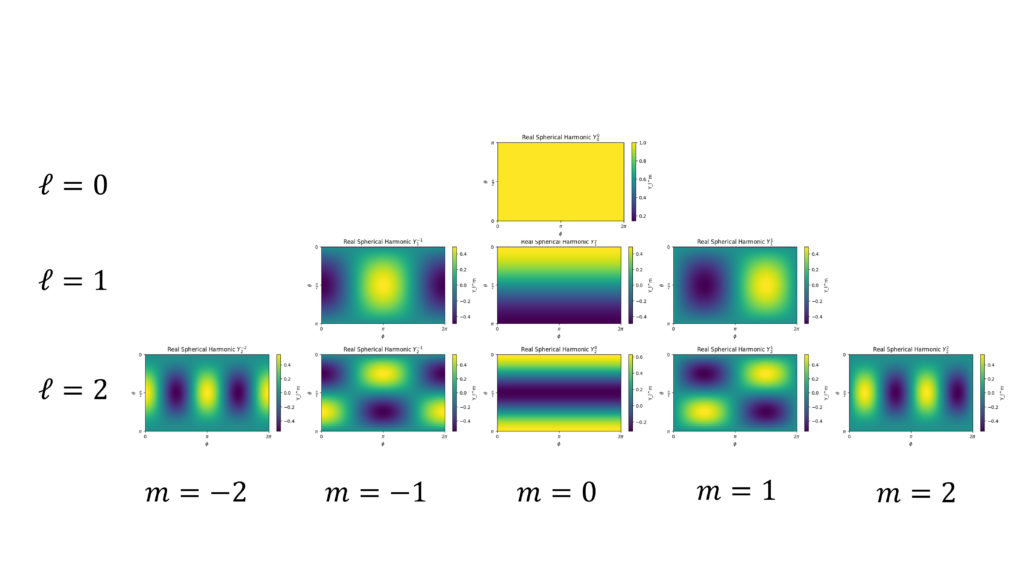
形としては縞模様のような形状を持ち、次数 $\ell$ が高くなるほど縞模様が細かくなっていくことが確認できます。また、位数 $m$ は球面プロットの図を含めると分布をちょっと回転させる形でバリエーションを作り出しているのがわかります。特に $m=1,-1$ を見れば、横方向($\phi$ 方向)にちょっとずらしたみたいなグラフであることがわかると思います。
SHの具体的な式
ここからはSHの具体的な式に入っていこうと思うのですが、一つ注意点としてSHの定義にはいくつかのバージョンが存在します。そのため、文献によってSHの定義が微妙に異なっていることがままあります(これで混乱した方は多いのではないでしょうか)。
その理由として次の2つの要素が挙げられます。
- 複素数と実数のバージョンがある
- 符号は実用上あってもなくてもよい
今回の記事ではその辺のバージョンが生まれた理由も含めて、1つずつ定義を解説していこうと思います。
複素数のSH
SHは最初に複素関数として定義されたという歴史的な経緯があり、そこから様々なバリエーションが生まれています。なので、まずは複素関数のSH, 複素SHから見ていきましょう。
複素SHは以下のような複素関数として定義されています。
$$
Y_{\ell}^m(\theta, \phi) = (-1)^{(m + |m|)/2} \sqrt{ \frac{2\ell + 1}{4\pi} \cdot \frac{(\ell – |m|)!}{(\ell + |m|)!} } \, P_{\ell}^{|m|}(\cos\theta) \, e^{im\phi} \tag{1.1}
$$
$P_\ell^m$ というのはルジャンドル陪多項式(Associated Legendre Polynomial)という実関数 $P_\ell^m \in \mathbb{R}$ です。具体的な形状としては次のように与えられています。
$$
P_{\ell}^{m}(x) = \frac{1}{2^{\ell}} (1 – x^2)^{m/2} \sum_{j=0}^{\lfloor(\ell – m)/2\rfloor}
\frac{(-1)^j (2\ell – 2j)!}{j!(\ell – j)! (\ell – 2j – m)!} x^{\ell – 2j – m} \tag{1.2}
$$
思わず「え?」と言いたくなるほど複雑な式ですが、今回の話では式を暗記する必要はありません。式の各要素について1つずつ注目して、その意味について理解していきましょう。
式 (1.1) はその役割によって以下のように大きく4つの要素に分けることができます。
\begin{align}
\text{符号部} & \, (-1)^{(m + |m|)/2} \tag{1.3} \\
\text{正規化係数} & \, \sqrt{ \tfrac{2\ell + 1}{4\pi} \cdot \tfrac{(\ell – |m|)!}{(\ell + |m|)!} } \\
\text{極角部} & \, P_{\ell}^{|m|}(\cos\theta) \\
\text{方位角部} & \, e^{im\phi}
\end{align}
ここでは便宜上それぞれ符号部、正規化係数、極角部、方位角部と呼ぶことにします。
符号部は単純に $m$ から符号を決定する要素です。もともとSHはラプラス方程式という方程式を由来としているため、その導出過程で符号部が生まれました。物理学などの分野では符号部に意味がありますが、3DCGの応用においては符号部は意味を持ちません(理由は後述)。なので、符号部を深く考える必要はありません。
次に正規化係数ですが、これはSHが正規性を持つための調整用の定数です。正規性については後述しますが、これがあるおかげでSHの議論がとてもシンプルに行うことができます。単なる調整でしかないため、これ自身に特別な意味があるというわけではありません。
文献によっては正規化係数をまとめて $N(\ell,m)$ として表示することもあります。
$$
N(\ell,m) = \sqrt{ \frac{2\ell + 1}{4\pi} \cdot \frac{(\ell – |m|)!}{(\ell + |m|)!} } \tag{1.4}
$$
残った極角部、方位角部はSHの本質的な要素です。それぞれ極角 $\theta$ 、方位角 $\phi$ の成分を担います。
極角部はルジャンドル陪多項式に対して、極角 $\theta$ のコサイン $\cos{\theta}$ を代入したものです。これがどんなものになるか見るため、それぞれ $\ell, m$ ごとに $P_{\ell}^{|m|}(\cos\theta)$ をプロットした図が次の通りです。縦軸を $\theta$、 横軸を $\phi$ としていて、-1から1の範囲で色を付けています(ものによってはこの範囲は超えます)。
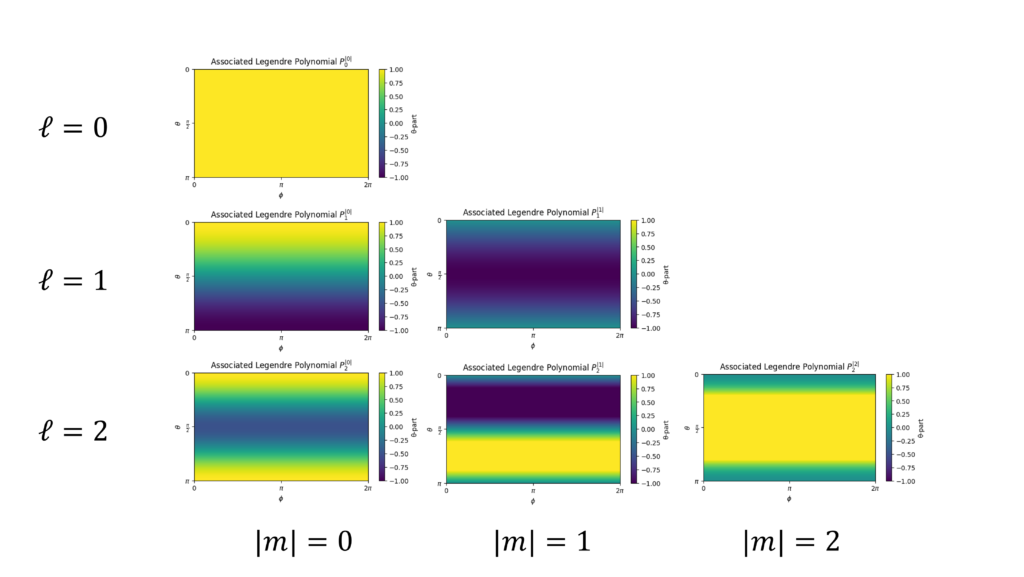
$\ell =0$ だけは特殊で完全な定数なのですが、$\ell = 1, 2$ と次数を上げていくと $\theta$ 方向に縞模様を作り出す関数として働いていることが分かると思います。この周期性自体は $\cos$ を引数としていることから来ていて、$P_{\ell}^{|m|}(\cos\theta)$ は極角 $\theta$ に対して周期的で、見た目上は図のような縞模様を成します。
この時、次数 $\ell$ はその縞模様における周波数に関係しており、次数 $\ell$ が上がるほど縞模様の周波数は高くなっていきます(細かくなる)。一方で位数 $m$ の作用は単純ではないものの、複雑なオフセットをかけることで新たにバリエーションを作り出していると解釈できるかなと思います。
次は方位角部の方について見てみましょう。
方位角部は $e^{im\phi}$ とシンプルな複素指数関数で、複素SHにおいては唯一の複素数を持つ要素です(それ以外は実数です)。
複素数なので分かりにくくなってしまっていますが、方位角部の持つ役割は実はとても単純です。複素数のオイラーの公式 $e^{i\Theta} = \cos{\Theta} + i \sin{\Theta}$ を思い出してもらえるとわかるように、方位角部は単に方位角方向の振動を表しています。
従って、SHは $\phi$ 方向で周期的に縞模様を作りだし、位数 $m$ というのはその振動における周波数の役割を持ちます。複素数なので直接プロットできませんが、試しに $\cos$ でそれぞれプロットしてみるとこんな感じです。実部と虚部はそれぞれ $\cos、\sin$ によって縞模様のような形状になります。
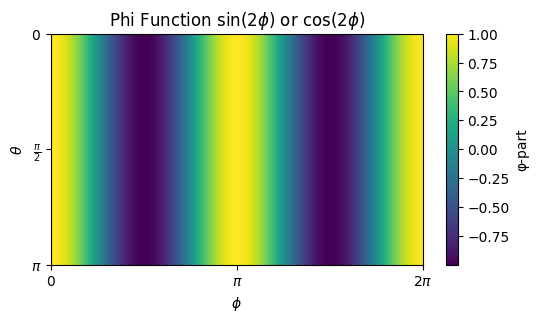
平たく言えば、その形状に注目すれば極角部と方位角部はそれぞれ縦方向、横方向に縞模様を作り出す関数です。従って、その乗算によってできるSHは格子上の縞模様のような形状を持つものになります。
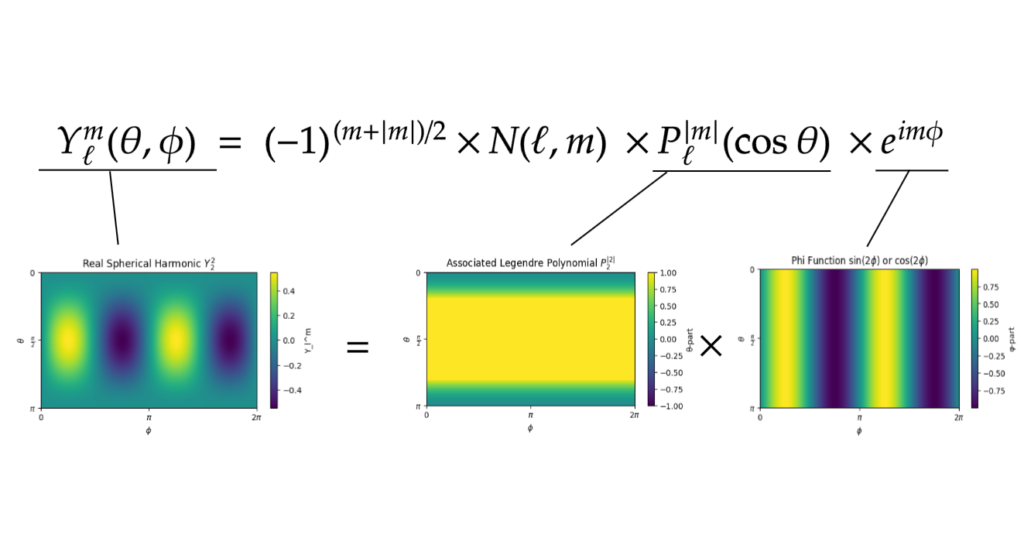
以上がSHの大まかな要素の説明になります。慣れてないと難しいと感じるかもしれませんが、なんとなくイメージが付いていれば大丈夫です。
複素SHを今後使う上で符号部は煩雑になるだけなので、以降は符号部を排除した複素SHを用いて議論していこうと思います。
$$
Y_\ell^m(\theta,\phi) =N(\ell,m) \, P_{\ell}^{|m|}(\cos\theta) \, e^{im\phi} \tag{1.6}
$$
今後のため1つだけ複素SHの性質を紹介します。それは $m=0$ の複素SHは実関数になると言うことです。$m=0$ の場合、唯一の複素数となる方位角部は常に1となるため、結果として複素SHは $Y_\ell^0$ は実関数となります。また、これは $Y_\ell^0$ が方位角 $\phi$ に依存しないことも意味します。このように $m=0$ の複素SH $Y_\ell^0$ は他のSHに比べると特殊な性質を持っています。
$$
Y_\ell^m(\theta,\phi) =
\begin{cases}
Y_\ell^m(\theta,\phi) \in \mathbb{C} & \text{if } m \neq 0 \\
Y_\ell^0(\theta) \in \mathbb{R} & \text{if } m = 0 \\
\end{cases}
\tag{1.7}
$$
更に特殊な話として、$Y_0^0$ は定数です。これに関しては $\theta$ も考える必要はありません。
$$
Y_0^0 = \frac{1}{2} \sqrt{\frac{1}{\pi}}
\tag{1.8}
$$
実数のSH
複素SHは物理学や証明など便利になることはあるのですが、3DCGのような主に実数を扱う分野では複素関数は少々過剰です。実数の範囲で収まるようなSHを考えたいと言うことで、実SHが考案されました。
その関係性はちょうど実フーリエ級数と複素フーリエ級数の関係性と同じです。実SHは複素SHの実部と虚部を取り出したものとして定義されます。
具体的な実SH $Y_{\ell,m}$ の定義は次のように与えられています。
$$
Y_{\ell,m} =
\begin{cases}
\sqrt{2} \Re[Y_\ell^m] & \text{if } m > 0 \\
Y_\ell^0 & \text{if } m = 0 \\
\sqrt{2} \Im[Y_\ell^{|m|}] & \text{if } m < 0
\end{cases}
\tag{2.1}
$$
$m$ によって定義が分岐し、$m$ が正なら実部 $\Re$、$m$ が負なら虚部 $\Im$、$m=0$ ならそのまま使う(元から実関数なので)というものになっています。ここで $\sqrt{2}$ がついているのはこれもまた正規化のためです。具体的な形状としては
$$
Y_{\ell,m} =
\begin{cases}
\sqrt{2} N(\ell,m) \, P_{\ell}^{|m}(\cos\theta) \, \cos(m\phi) & \text{if } m > 0 \\
Y_\ell^0 & \text{if } m = 0 \\
– \sqrt{2} N(\ell,m) \, P_{\ell}^{|m|}(\cos\theta) \, \sin(m\phi) & \text{if } m < 0
\end{cases}
\tag{2.2}
$$
という形になります(導出はここでは省略します)。
$e^{im\phi} = \cos{m\phi} + i \sin{m\phi}$ であることを考えれば、納得しやすいと思います。
ここでも符号は意味はないため、CG分野では完全に符号を取り除いた次のような形式が取られるのをよく見ます。$m$ に絶対値つけたり付けなかったりは割と文献によります。
$$
Y_{\ell,m} =
\begin{cases}
\sqrt{2} N(\ell,m) \, P_{\ell}^{m}(\cos\theta) \, \cos(m\phi) & \text{if } m > 0 \\
Y_\ell^0 & \text{if } m = 0 \\
\sqrt{2} N(\ell,m) \, P_{\ell}^{|m|}(\cos\theta) \, \sin(|m|\phi) & \text{if } m < 0
\end{cases}
\tag{2.3}
$$
SHの性質
SHは複雑な関数ではありますが、球面上の関数として良い性質を持っています。いくつかありますが、一番重要なのが完全正規直交関数系を成すことです。
これはSHは任意の球面上(方向)の関数を自身の組み合わせによって表現することができる1ことを示しています。平たく言えば、球面上でフーリエ級数展開的なことができるというわけです。
直交展開
関数にはベクトルのように内積という概念が存在します。定義域 $D$ で定義されたある関数 $f(x),g(x), x \in D$ に対して、その内積 $\langle g,h \rangle$ は $f,g$ の積に対する範囲 $D$ の積分として表されます。
$$
\langle g,h \rangle = \int_D g(x) h(x) dx
\tag{3.1}
$$
特に内積 $\langle g,h \rangle$ が0となる時、その関数 $g,h$ は直交している(Orthogonal)と表現します。
いくつもの関数 $g_1, g_2, g_3, … $ を集めた関数列 $[g_1, g_2, g_3, …, g_i, …]$ で、異なる関数での内積が0、自分自身との内積が0以外であった場合、これを直交関数系と呼びます。
$$
\langle g_i, g_j \rangle
\begin{cases}
= 0 & \text{if } i \neq j \\
\neq 0 & \text{if } i = j \\
\tag{3.2}
\end{cases}
$$
特に、自身との内積の値が1である場合は正規直交関数系と呼びます。
$$
\langle g_i, g_j \rangle
\begin{cases}
= 0 & \text{if } i \neq j \\
= 1 & \text{if } i = j \\
\tag{3.3}
\end{cases}
$$
if文で分けるのは表記的に大変なので今後はクロネッカーのデルタ関数 $\delta_{i,j}$ を使います。
$$
\langle g_i, g_j \rangle = \delta_{i,j}
\tag{3.4}
$$
このような内積を考える理由はベクトルの概念を関数へと拡張するためです。内積が定義されることで、うまいことベクトルで使われていた概念が関数にも導入することができます。
今回の話で関係あるのが、ベクトル空間(内積空間)における直交基底という概念です。$n$ 次元ベクトル空間 $V$ では、直交基底 $e_1, e_2, …, e_n $ が与えられていると、$V$ の任意のベクトルというのはどれであろうとも直交基底の線形結合として表すことができます。その時、各基底における係数を $a_1, a_2, …, a_n $ とすると、$x \in V$ は
$$
x = a_1 e_1 + a_2 e_2 + … + a_n v_n
\tag{3.5}
$$
というように書くことができます。
もちろん、必ずしも基底は直交する必要はありませんが、直交基底の場合、各係数 $a_i$ は $x$ と $e_i$ の内積として容易に求めることができます。
$$
a_i = x \cdot e_i
\tag{3.6}
$$
ここで重要なのは直交した基底があれば、それらの線形結合で(ベクトル空間の範囲で)多種多様なベクトルを容易に作り出すことができるという点です。このアイディアを関数へと拡張します。
ベクトルの直交基底のように、直交する関数たちを集めた関数列 $[g_1, g_2, g_3, …]$ を使い、ある関数 $f(x)$ を直交関数系 $g_i(x)$ の線形結合で表現することを考えます。
$$
f(x) = f_1 g_1(x) + f_2 g_2(x) + f_3 g_3(x) + ….
\tag{3.7}
$$
各係数 $f_i$ は直交性から $f$ と $g_i$ の内積から求めることができます。
$$
f_i = \int_D f(x) g_i(x) dx
\tag{3.8}
$$
これを直交展開(Orthogonal Expansion)と呼びます。関数 $f$ が難しい形をしていたとしても、直交展開することで別の性質が良い直交関数たちとして表現することができます。
とはいえ、実際に直交展開できるかはもちろん直交展開ができるかどうかは関数列 $[g_1,g_2, g_3,…]$ によります(+関数 $f$ が自乗可積分関数であること)。
様々な関数を余すことなく再現しなければならないので、なかなか厳しい条件が課せられます。ちゃんと直交展開が可能な関数列である場合、その関数列は完全である(Complete)と表現されます。特に完全かつ正規直交であればまとめて、その関数列を完全正規直交関数系と言います
完全正規直交関数系の代表例としてはフーリエ級数が挙げられます。
これは $[1, \cos{x},\cos{2x}, … ,\sin{x}, $ $ \sin{2x}, …]$ という定数と三角関数を集めた関数列を基底として扱ったものです(周期 $2\pi$ のフーリエ級数)。
これらは正規直交でありかつ完全であることが証明されているため、周期 $2\pi$ の関数 $f(x)$ を三角関数+定数の線形結合として表現することができます
$$
f(x) = a + b_1 \cos{x} + b_2 \cos{2x} + … + c_1 \sin{x} + c_2 \sin{2x} + …
\tag{3.9}
$$
係数の計算も直交性から次のように求められます。
$$
\begin{align}
a &= \int_0^{2\pi} f(x) dx \\
b_i &= \int_0^{2\pi} f(x) \cos{i x}dx \\
c_i &= \int_0^{2\pi} f(x) \sin{i x} dx \\
\end{align}
\tag{3.10}
$$
フーリエ級数の応用は皆さんご存じのとおり非常に多岐にわたります。シンプルに関数の単純化として利用されることもありますが、特に面白い点として画像処理の分野では画像に対して周期性という新しい視点を与えました。
SH展開
それで SH$[Y_0^0, Y_1^{-1}, Y_1^0, Y_1^1, …]$ はありがたいことに完全正規直交関数系であることが知られています(複素、実SH共に)。2つの任意のSHをかけたものを球面上 $S^2$ で積分すると、 次数 $\ell$ と位数 $m$ が一致した場合1、一致しなかったら0と、直交性を持ちます(完全性も証明されています)。
$$
\int_{S^2} Y_\ell^m Y_{\ell’}^{m’} d \omega= \delta_{\ell, \ell’} \delta_{m, m’}
\tag{4.1}
$$
$$
\int_{S^2} Y_{\ell,m} Y_{\ell’,m’} d \omega= \delta_{\ell, \ell’} \delta_{m, m’}
\tag{4.2}
$$
そのため、SHによる直交展開が可能です。実SHに着目して、ある球面上の関数 $f : S^2 \rightarrow \mathbb{R}$ があった時、この関数はSH $Y_{\ell,m}$ とそれに対応する何らかの係数 $f_{\ell,m}$ によって次のように展開することができます。今回の記事では、これをSH展開と呼ぶことにします。
$$
\small
f_{\ell, m}(\omega) = f_{0,0} Y_{0,0}(\omega) + f_{1,-1} Y_{1,-1}(\omega) + f_{1,0} Y_{1,0}(\omega) + f_{1,1} Y_{1,1}(\omega) + f_{2,-2} Y_{2,-2}(\omega) + … \tag{4.3}
$$
それぞれのSHにおける係数 $f_{\ell,m}$ は、対応するSH $Y_{\ell,m}$ と目的の関数 $f$ を球面 $S^2$ で積分した結果として定義されています。これらを求めておけば $f$ をSHで再現することができるというわけです。
$$
f_{\ell,m} = \int_{S^2} f(\omega) Y_{\ell,m}(\omega) d\omega \tag{4.4}
$$
SH展開において重要なこととして、目的の関数 $f$ が方位角 $\phi$ に依存しない場合は $m \neq 0$ のSH係数は0となります。例えば $m>0$ の実SHで(3.4)式に従って計算してみると、重積分の分解によって $\phi$ の積分は $\cos$ だけになります。
$$
\begin{align}
f_{\ell,m} &= \int_{S^2} f(\omega) Y_{\ell,m}(\omega) d\omega \\
&= \int_{0}^{\pi} \int_{0}^{2\pi} f(\theta) Y_{\ell,m}(\theta, \phi) \sin{\theta} d\phi d\theta \\
&= \int_{0}^{\pi} \int_{0}^{2\pi} f(\theta) \sqrt{2} N(\ell,m) P_{\ell}^{|m|} (\cos{\theta}) \sin{\theta} \cos{(m \phi)} \, d\phi d\theta \\
&= \int_{0}^{\pi} f(\theta) \sqrt{2} N(\ell,m) P_{\ell}^{|m|} (\cos{\theta}) \sin{\theta} d\theta \int_{0}^{2\pi} \cos{(m \phi)} \, d\phi \\
\end{align}
\tag{4.5}
$$
この $\phi$ の部分の積分は計算してみたらわかるように0となります。すなわち、$m > 0$ ではSHの係数は0となります。
同様に $m < 0$ でも調べることができ、$m \neq 0$ のSH係数は全て0になり、$m = 0$ だけの係数が残ります(これは後でちょっと出てくるので覚えておいてください)。
$$
f_{\ell,m} =
\begin{cases}
0 & \text{if } m \neq 0 \\
f_{\ell,0} & \text{if } m = 0 \\
\end{cases}
\tag{4.6}
$$
符号と直交性
SHの紹介の際に実用上符号は意味をなさないという話をしました。これは直交性が符号に依存しないことと、3DCGの主な応用先がSH展開であることに由来します。
まず、直交している関数に対して符号を反転させても直交性は維持されます。
例えば、あるSH $Y_{L, M}$ だけを反転させた新しいSH $Y_{0,0},…,-Y_{L,M}, …$ は、変わらず正規直交系を成します。これは計算すればわかることで、$\ell \neq L$, $m \neq M$ では
$$
\int_{S^2} Y_{\ell,m} (- Y_{L,M}) d\omega = – \int_{S^2} Y_{\ell,m} Y_{L,M} d\omega = 0
\tag{5.1}
$$
同じ $-Y_{L,M}$ 同士では
$$
\int_{S^2} (- Y_{L,M}) (- Y_{L,M}) d\omega = \int_{S^2} Y_{L,M} Y_{L,M} d\omega = 1
\tag{5.2}
$$
というように直交性は何一つ変わることがありません。
従って、新しいSHでもSH展開することができます。元々のSHによる展開が以下のように示されていたら
$$
f = f_{0,0} Y_{0,0} + … + f_{L,M} Y_{L,M} + …
\tag{5.3}
$$
新しいSHにおけるSH展開をしてみると、全く同じ関数を展開しているわけですから係数 $f_{L,M}$ の符号が反転した以下の形で表現されます。
$$
f = f_{0,0} Y_{0,0} + … + (- f_{L,M}) (-Y_{L,M}) + …
\tag{5.4}
$$
SH係数というのは正であるとかの符号に関する条件は何もないため、正直SH係数が負になろうが正になろうが別に異常でもなんでもなく、単に「そういう値」でしかありません。新しいSHで復元したいなら、符号が反転しただけの $- f_{L,M}$ という値を保持すればいいだけです。
なので、SH展開を扱う場合は係数の符号やSHそのものの符号というのは興味がなく、符号をどう扱っても問題がないわけです。3DCGにおいてはSH展開が主な応用先であるため、符号部を省いたSHの定義がよく使われています。
SHの回転
SHの面白い性質としてもう一つ、回転があります。
SHに原点周りの回転 $\mathcal{R}$ をかけた場合、座標 $(\theta,\phi)$ を $\mathcal{R}$ によって変換した $(\theta, \phi) \rightarrow \mathcal{R}(\theta,\phi)$ ものとして扱います。つまり、変換後のSHは $Y_{\ell,m}(\mathcal{R}(\theta,\phi))$ と書くことができます2。
この回転後のSH $Y_{\ell,m}(\mathcal{R}(\theta,\phi))$ は、回転前の同次数SH $Y_{\ell,m}(\theta,\phi)$ の線形結合によって表現できるという性質があります。具体的にはある回転 $\mathcal{R}$ に対する、位数 $m$ と $m’$ 間の係数を $D_\ell^{m,m’}(\mathcal{R})$ とすると、次のような式が成り立ちます
$$
Y_{\ell,m}(\theta’,\phi’) = \sum_{m’ = -\ell}^\ell D_\ell^{m,m’}(\mathcal{R}) Y_{\ell,m’}(\theta,\phi) \tag{6.1}
$$
例として $\ell = 1$ のSHに対して何かしらの回転 $\mathcal{R}$ をかけたとすると、それぞれの回転後のSHは次のようになります。同じ次数 $\ell = 1$ のSHを組み合わせる形で表現でき、そのウェイトが $D_\ell^{m,m’}(\mathcal{R})$ となっています。
$$
\small
\begin{align}
Y_{1,-1}(\mathcal{R}(\theta,\phi)) &= D_1^{-1,-1}(\mathcal{R}) Y_{1,-1}(\theta,\phi) + D_1^{-1,0}(\mathcal{R}) Y_{1, 0}(\theta,\phi) + D_1^{-1,1}(\mathcal{R}) Y_{1,1}(\theta,\phi) \\
Y_{1,0}(\mathcal{R}(\theta,\phi)) &= D_1^{0,-1}(\mathcal{R}) Y_{1,-1}(\theta,\phi) + D_1^{0,0}(\mathcal{R}) Y_{1,0}(\theta,\phi) + D_1^{0,1}(\mathcal{R}) Y_{1,1}(\theta,\phi) \\
Y_{1,1}(\mathcal{R}(\theta,\phi)) &= D_1^{1,-1}(\mathcal{R}) Y_{1,-1}(\theta,\phi) + D_1^{1,0}(\mathcal{R}) Y_{1,0}(\theta,\phi) + D_1^{1,1}(\mathcal{R}) Y_{1,1}(\theta,\phi)
\end{align}
\tag{6.2}
$$
具体的な $D_\ell^{m,m’}(\mathcal{R})$ の値は回転によって異なるのですが、意味としてはある種のSHの回転行列に相当します。上の式を行列に置き換えたら感覚的に分かりやすいかと思います(今回の記事では具体的な値について取り扱いません)。
$$
\small
\begin{pmatrix}
Y_{1,-1}(\mathcal{R}(\theta,\phi)) \\
Y_{1,0}(\mathcal{R}(\theta,\phi)) \\
Y_{1,1}(\mathcal{R}(\theta,\phi))
\end{pmatrix}
=
\begin{pmatrix}
D_1^{-1,-1}(\mathcal{R}) & D_1^{-1,0}(\mathcal{R}) & D_1^{-1,1}(\mathcal{R}) \\
D_1^{0,-1}(\mathcal{R}) & D_1^{0,0}(\mathcal{R}) & D_1^{0,1}(\mathcal{R}) \\
D_1^{1,-1}(\mathcal{R}) & D_1^{1,0}(\mathcal{R}) & D_1^{1,1}(\mathcal{R})
\end{pmatrix}
\begin{pmatrix}
Y_{1,-1}(\theta,\phi) \\
Y_{1, 0}(\theta,\phi) \\
Y_{1, 1}(\theta,\phi)
\end{pmatrix}
\tag{6.3}
$$
全体を含めて行列にすると画像のようなブロック対角行列となります($\ell = 0$ だけは回転に不変なので1)。とりあえず、ここではSHの回転は同じ次数のSHと何かしらの係数の線形結合で表せる、ということだけ覚えてくれれば大丈夫です。
3DCGの応用について
では、これが何に使えるのかという話です。
3DCGにおける照明計算ではよく方向の関数が出てきます。反射の分布を示すBRDFは入射方向($\omega_i$)と出射方向($\omega_o$)の関数 $f(\omega_i, \omega_o)$ として表されますし、はたまた出射光の輝度 $L_o$ も理論的には出射方向や法線 $n$ の関数 $L_o(\omega_o, n)$ として扱うことができます。
となれば、方向の関数に対するSH展開を使ってあげれば、なんかいい感じのことができそうだと感じます。そんな理由で3DCGにSHというものが現れるわけです。
UnityなどにあるLight Probeは本来であればTextureとして保存すべき情報をSHによって圧縮をしています。
今回はLight ProbeにおけるSHの圧縮について解説していこうと思います。
Light Probeは何をしたいのか
まず、Light Probeというのはそもそも何をするものかというと、空間中に放射照度(Irradiance)と呼ばれる量を保存するものです。Irradianceというのは(単位時間あたりに)物体の表面へ照射された光の単位面積当たりのエネルギーを表すもので、応用上ではDiffuse反射の計算に使われる物理量です。
Irradianceは面が向いている向き(法線)によって変わるため、数式としては位置 $x$ と法線 $n$ の関数 $E(x,n)$ と書かれます。具体的には次のような積分として定義されています。
$$
E(x,n) = \int_{\Omega(n)} \frac{1}{\pi} (n \cdot \omega_i) \, L_i(\omega_i) d\omega_i \tag{7.1}
$$
正確には $\pi$ を除いた以下の積分値が物理学的な定義でのIrradianceなのですが、3DCGでは割り算の計算コスト削減のため $\pi$ を含めた(7.1)式を考えることが多いです。これ自体も3DCGではIrradianceと呼ばれます。
$$
\int_{\Omega(n)} (n \cdot \omega_i) \, L_i(\omega_i) d\omega_i \tag{7.2}
$$
$L(\omega_i)$ は $\omega_i$ という入射方向から来た光の輝度(明るさ)を表すもので、 $\Omega(n)$ は $n$ 方向を向いている図のような半球面を表しています。
$\Omega_i$ は面の反対側を向く方向 $n \cdot \omega_i < 0$ を排除するという意味で定義されています。要は裏側から来る光は排除して、色々な方向から来る光のエネルギーを計算しているというものです。
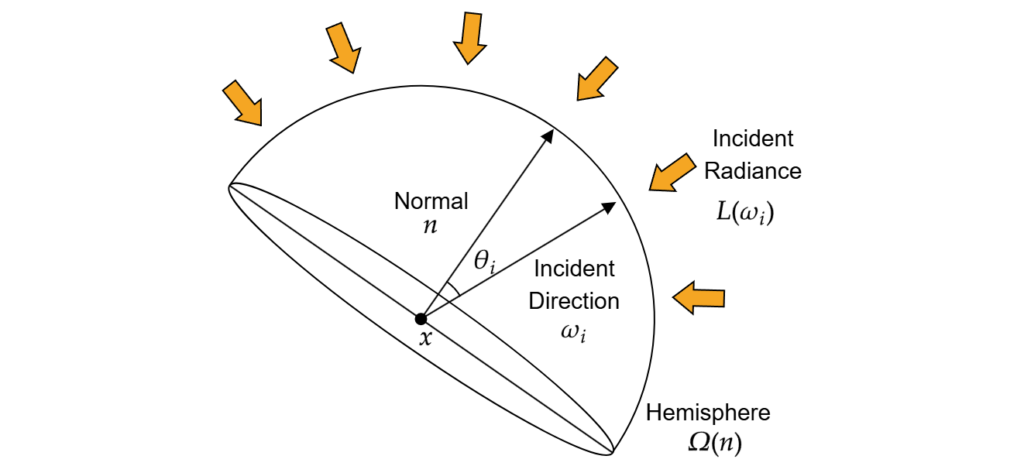
あらゆる位置 $x$、法線 $n$ でこのIrradianceを保持することを目的として、Light Probeはある位置 $x_i$ におけるIrradianceの関数 $E(x_i,n)$ そのものを保存します。
なぜIrradianceを保存するのかと言えば、Diffuse反射を計算するためです。Diffuse反射の式を追っていくと殆どIrradianceで構成されており、それさえ計算できればDiffuse反射を求めることができるというような関係性を持ちます。
実際どのような関係性なのかDiffuse反射の式からちゃんと考えてみましょう。
法線 $n$ のシェーディング点 $x$ における出射方向 $\omega_o$ 方向のDiffuse反射 $L_{\mathrm{diffuse}} (\omega_o,n)$ はレンダリング方程式から次のように与えられます。
$$
L_{\mathrm{diffuse}}(x, n) = \int_{\Omega(n)} \frac{\rho(x)}{\pi} \, (n \cdot \omega_i) \, L_i(\omega_i) d\omega_i \tag{7.3}
$$
ここで $\rho$ というのはアルベド(ベースカラー)を意味しています。
馴染みがない人だと分かりづらいかもしれませんが、これの意味することは非常に単純です。ある方向 $\omega_i$ から輝度(明るさ)$L_i(\omega_i)$ の光が来た時、$\omega_o$ 方向に飛ぶDiffuse反射光は次のように表されます(正確ではありませんが意味としてはこんなものです)。
$$
d L_{\mathrm{diffuse}}(x, n) = \frac{\rho(x)}{\pi} \, (n \cdot \omega_i) \, L_i(\omega_i) d\omega_i \tag{7.4}
$$
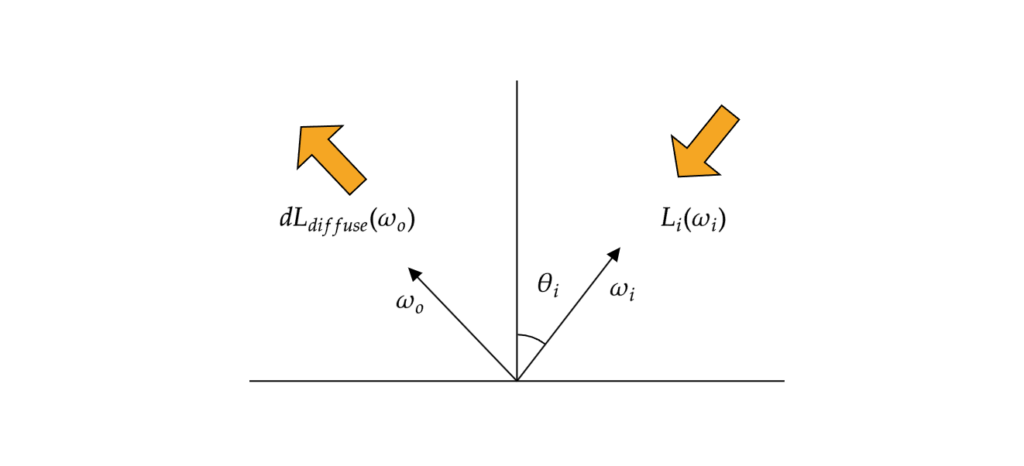
方向 $\omega_i$ から来た反射光の値は(7.4)式で表せるため、あらゆる方向($=\Omega(n)$)でそれらをかき集めれば、反射光全体の輝度が分かるはずです。(7.3)式はそれを積分という形で表しています。
実際これを計算するには入射光 $L_i$ が厄介で、あくまで $\omega_i$ から来る光以上の制限はないので光源からの直接光もあれば、何度も反射してやってくる間接光も含まれています。要はGlobal Illuminationを計算しないと $L_i$ の具体的な値はわからないわけです。なので、リアルタイムレンダリングではこの部分を事前計算する手法が取られることが多いです。
一般に物体の色 $\rho$ は別途Textureなどで与えられるため、これを外した積分、つまりはIrradiance
$$
E(x,n) = \int_{\Omega(n)} \frac{1}{\pi} (n \cdot \omega_i) \, L_i(\omega_i) d\omega_i \tag{7.5}
$$
は位置 $x$ と法線 $n$ が決まっていれば、シンプルにパストレーシングなどの数値計算手法を使って事前計算することができます。Irradianceの値さえわかれば、$\rho$ をかけるだけでDiffuse反射の値 $L_{\mathrm{diffuse}}$ が得られます。
$$
L_{\mathrm{diffuse}}(x,n) = \rho(x) E(x,n) \tag{7.6}
$$
これでIrradianceの重要性が分かったかと思います。
従って、我々がすべきことはこのIrradiance $E(x,n)$ を計算し、$E(x,n)$ をどうにかして保存することです。代表的なIrradianceの保存方法としてはLight Mapが挙げられます。Light Mapはジオメトリの表面におけるIrradianceをTextureとして格納するものです。

Light Mapに格納された値 $E_{\mathrm{lightmap}}$ はIrradianceそのものであり、最終的に色 $\rho$ と掛け合わせることでDiffuse反射の計算を行っています。
$$
E_{\mathrm{lightmap}}(n, x) = \int_{\Omega(n)} \frac{1}{\pi} (n \cdot \omega_i) \, L_i(\omega_i) d\omega_i \tag{7.7}
$$
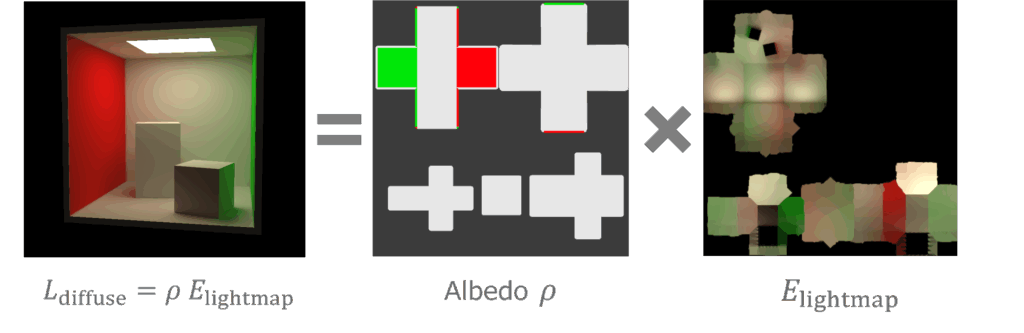
しかし、Light Mapはかなり限定的な保存形式です。完全に位置と法線 $x,n$ を固定してしまっているため、特にランタイムに動くDynamicなオブジェクトにLight Mapを適用することはできません。
理想的にはあらゆる位置 $x$、あらゆる法線 $n$ に応じたIrradiance $E(x,n)$ を保存することがベストです。その考えに基づいて、代表的な位置で保存したのがLight Probeというわけです3。
Light ProbeからDiffuse反射を求めたい場合は、まず自身の位置 $x$ から近くのProbe $x_i$ を検索し、法線 $n$ から対応するIrradiance $E(x_i, n)$ を取得します(実際はProbe間で補間をします)。そのIrradiance$E$ と物体の色 $\rho$ を使えば、Diffuse反射の値を求めることができます。
$$
L_{\mathrm{diffuse}}(x,n) = \rho(x) E(x_i, n) \tag{7.8}
$$
ここで、問題なのがLight Probeに保存するIrradiance $E(x_i,n)$ の保存形式です。
Light ProbeにおけるIrradianceはあらゆる法線 $n$ が角度 $\theta = 0^\circ, \phi = 45^\circ$ であっても、$40^\circ, 120^\circ$ であっても、はたまた $52^\circ, 233^\circ$ であっても、ちゃんと値を返さなければなりません。つまりは $E(x_i,n)$ という法線 $n$ の関数そのものを保存する必要があるわけです。
1つの手として、360°カメラのようにTextureでIrradianceを保存する方法が考えられます。こうしたIrradianceを保存したTextureのことをIrradiance Environment Mapと呼ぶみたいです(長いのでIrradiance Mapと呼びます)。実際の作品に使われていたかは定かではありませんが、研究の分野では少なくとも使われていたみたいです。
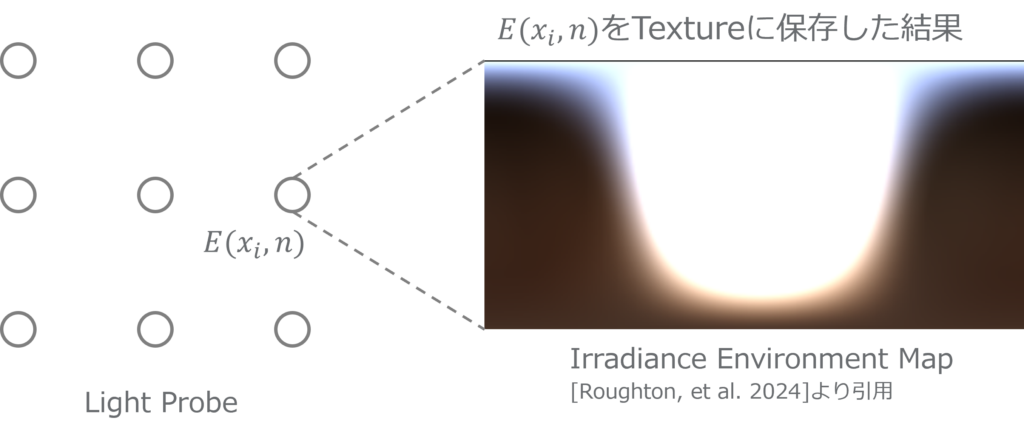
しかしながら、256×256ぐらいの低解像度で保存したとしても256×256個のtexelにRGBチャンネル3つ分、そしてLight Probeの数がかかってくるため、Float精度であれば 65536 x Light Probe数 x 32 bitとかなりの容量を食うことになります。正直、今ならギリギリ何とかなりそうではありますが、少なくともLight Probeを気軽に置くことができないでしょう。
どうにかして容量を削減したいところです。
Irradiance Mapの結果を見てみると、環境光が複雑であってもかなりボヤっとした画像になります。シンプルに画像としてみた時、Irradiance Mapは低周波成分が強い画像として見なすことができます。そこで高周波成分を取り除くことでデータの圧縮ができないかというアイディアが出てきます。
RamamoorthiとHanrahanという方々はそこに着目し、Irradiance Mapを低次数のSHを使って近似するという手法が2002年に発表されました [Ramamoorthi, Hanrahan. 2002]。
これによる圧縮結果は人間の目ではほとんどわからないぐらい品質が高いです。実際、見てみるとほとんど違いが分かりません。

この手法では $\ell = 2$ までのSHで近似するので、1 + 3 + 5で計9個のSHの係数で1channel分、それがRGB分あるのでたった27個のパラメーターでIrradianceを保存することができます。先ほどの例で出したTextureで比べれば300倍近くも圧縮ができているわけです。
現在のLight Probeはこの圧縮方法をつかってIrradianceの保存をし、Shader内でSHからIrradianceの復元を行ってDiffuseの反射計算を行っています。
Irradiance Environment Mapの近似
どのようにしてIrradianceをSHで近似していくのか、式を見つつ追っていきましょう。
SH係数の計算
まず、目的となる関数というのは Irradiance$E(n)$ です。Irradiance$E(n)$ の具体的な形状は次のように与えられています。
$$
E(n) = \int_{\Omega(n)} (n \cdot \omega_i) \, L_i(\omega_i) d\omega_i \tag{8.1}
$$
$E(n)$ というのは法線 $n$、つまりは方向を引数とする関数です。したがって、$E(n)$ はSHによって展開して次のように求められます。
$$
E(n) = E_{0,0} Y_{0,0}(n) + E_{1,-1} Y_{1,-1}(n) + E_{1,0} Y_{1,0}(n) + E_{1,1} Y_{1,1}(n) + … \tag{8.2}
$$
簡単のため、今後は総和記号を使って以下のように省略することにします(単にまとめただけなので特別な意味とかはありません)。
$$
E(n) = \sum_{\ell,m} E_{\ell,m} Y_{\ell,m}(n) \tag{8.3}
$$
SH係数の導出はでやったように $E(n)$ と $Y_{\ell,m}$ によって次のような積分値を求めれば得られます。
$$
E_{\ell,m} = \int_{S^2} E(n) Y_{\ell, m}(n) dn \tag{8.4}
$$
これさえ事前に計算できていれば、$E(n)$ を(8.3)によって復元することができます。
とは言え、なかなかにこれを解くのは難しいです。なぜかと言えば $E(n)$ 自体が積分であるため、展開すると最終的に二重の積分を計算する必要があるためです。
$$
E_{\ell,m} = \int_{S^2} \left( \int_{\Omega(n)} (n \cdot \omega_i) \, L_i(\omega_i) d\omega_i \right) \, Y_{\ell, m}(n) dn \tag{8.5}
$$
割と愚直に数値計算してもどうにかなりそうな感じではありますが、論文では面白いことにSHの性質を使ってより単純な形でSH係数を計算できるようにしています。
$E(n)$ の積分の範囲は現状 $n$ に依存した半球面 $\Omega(n)$ にしていますが、依存しているのもやりづらいので球面 $S^2$ へと拡張して統一的にやることにします。内積に対して $\max$ を使えば、積分値を変えずに拡張することができます(元々 $\Omega(n)$を 考えたのは内積値が負になる部分の計算を省くためでした)。
$$
\int_{\Omega(n)} (n \cdot \omega_i) \, L_i(\omega_i) d\omega_i = \int_{S^2} \max(n \cdot \omega_i, 0) \, L_i(\omega_i) d\omega_i \tag{8.6}
$$
被積分関数の内積部分を $A(n, \omega)$ と書くことにします。
$$
A(n, \omega) = \max(n \cdot \omega, 0) \tag{8.7}
$$
特に $n$ がup-vector、ここではZ軸に向いた法線 $n = (0, 0, 1)$ における $A(n,\omega)$ を $A(\omega)$ と書くことにします。$\omega$ の極角は $\theta_\omega$ と表記します。
$$
A(\omega) = \max((0, 0, 1) \cdot \omega, 0) = \max(\cos{\theta_\omega}, 0) \tag{8.8}
$$
まとめると、Irradiance $E(n)$ は次のような関数として表記されます。
$$
E(n) = \int_{S^2} A(n,\omega_i) \, L_i(\omega_i) d\omega_i \tag{8.9}
$$
この形状の積分は畳み込み積分と呼ばれるものに分類されます(らしい)。フーリエ変換では畳み込み積分のフーリエ変換は被積分関数のフーリエ変換の積として表現されたりと、畳み込み積分では被積分関数と積分後の結果にある程度の関係性が与えられることが多いです。
SHでも似たような話があり、$E$ のSH係数 $E_{\ell,m}$ は $A$ と $L_i$ をSH展開したときのSH係数によって求めることができるということが示されています(この証明は結構長いので省略します)。
$L_i$ は単なる方向の関数 $L_i(\omega)$ でしかないため、特に問題なくSH展開することができます。
$$
L_i(\omega) = \sum_{\ell,m} L_{\ell,m} Y_{\ell,m}(\omega) \tag{8.10}
$$
$$
L_{\ell,m} = \int_{S^2} L_i(\omega) Y_{\ell,m}(\omega) \, d\omega \tag{8.11}
$$
$L_i$ は各方向における入射光の値であり、その値はいわゆるGIを計算することで求めることができます。実装上ではパストレーシングなどを使用して計算することが可能なはずです。なので、ここのSH係数 $L_{\ell,m}$ は事前計算で求めることができます。
一方で $A$ については $n$ と $\omega$ と2つの方向を考えているため、どうするか悩むとこでありますが、$n = (0, 0, 1)$ の状況における $A(\omega)$ のSH係数で良いとのことです。これは何故かというと軸を合わせるように回転させることを考えて、$n=(0, 0, 1)$ の状況へと帰結するように証明が建てられているためです。
その場合であれば $A$ はシンプルに $\omega$ の関数なのでSH展開することができます。
$$
A(\omega) = \sum_{\ell,m} A_{\ell,m} Y_{\ell,m}(\omega) \tag{8.12}
$$
$$
A_{\ell,m} = \int_{S^2} A(\omega) Y_{\ell,m}(\omega) \, d\omega \tag{8.13}
$$
ここで重要なのが $m \neq 0$ のSH係数はすべて0になるというところです。
$A(\omega)$ の具体的な値は極角 $\theta_\omega$ で $A(\omega) = \max(\cos{\theta_\omega}, 0)$ のため、方位角 $\phi_{\omega}$ に依存しません。したがって、$m \neq 0$ であるSH係数は0にならざるを得ません。よって、
$$
A(\omega) = \sum_{\ell} A_{\ell,0} Y_{\ell,0}(\omega) \tag{8.14}
$$
となります。このことから $m$ の添え字を排除して $A_{\ell} = A_{\ell,0}$ と表記することがあります。
以上で必要な情報がまとまりました。SH係数 $E_{\ell,m}$ は $A_{\ell}, L_{\ell,m}$ に関して、次のような等式が成り立つことが証明されています。
$$
E_{\ell,m} = \sqrt{\frac{4\pi}{2 \ell + 1}} A_{\ell} L_{\ell,m} \tag{8.15}
$$
これはつまり、$A_\ell, L_{\ell,m}$ さえ求められていれば目的のSH係数 $E_{\ell,m}$ をシンプルな掛け算で簡単に求められるということです。
$A_{\ell}$ は解析解が既に求められており、定数と一緒に $\hat{A}_\ell$ とまとめられます(具体的な値はAppendix参照)。
$$
\hat{A}_\ell = \sqrt{\frac{4\pi}{2 \ell + 1}} A_{\ell} \tag{8.16}
$$
よって、私たちが本質的にすべきことは入射光 $L_i$ に対するSH係数 $L_{\ell,m}$ の事前計算だけです。これは(8.11)式で与えられており、(8.5)と比べればはるかに計算しやすいです。こうしたIrradianceのSH係数の計算は式(8.15)によってシンプルかつ、高速に計算できるようにしています。
SHによる近似
こうしてIrradiance MapのSH展開を求められるようになりました。Light Probeはここから低次のSHを取り出して、Irradiance Mapの近似を行います。
SHによる近似では $\ell = 0$ までの項をL0、$\ell = 1$ の項をL1、$\ell = 2$ の項をL2と、次数 $\ell$ ごとにL0, L1, L2, …と呼びます。一般的なLight ProbeではL2までを使用します(場合によってはL1までというのもあります)。
従って、Light Probeは $E_{0,0}, E_{1,-1}, E_{1, 0}, E_{1, 1}, E_{2, -2}, E_{2, -1},E_{2,0},E_{2,1},E_{2,2}$ の計9つのSH係数を保持します。Light Probeからこの値をもらったとして、法線 $n$ のIrradiance $E(n)$ を求めるとなると
$$
\begin{align}
E(n) &\approx E_{0,0} Y_{0,0}(n) \\
&+ E_{1,-1} Y_{1,-1}(n) + E_{1, 0} Y_{1,0}(n) + E_{1, 1} Y_{1,1}(n) \\
&+ E_{2, -2} Y_{2,-2}(n) + E_{2, -1} Y_{2,-1}(n) + E_{2,0} Y_{2,0}(n) \\
&+ E_{2,1} Y_{2,1}(n) + E_{2,2} Y_{2,2}(n)
\end{align}
\tag{9.1}
$$
という形でIrradiance Mapの近似を行っています。
式上では納得できるかもしれませんが、このSH近似は視覚上どのように行われているのか気になるところです。その辺は [Ramamoorthi, Hanrahan. 2002] のfigure4で詳しく説明されています。その図を以下に引用します。
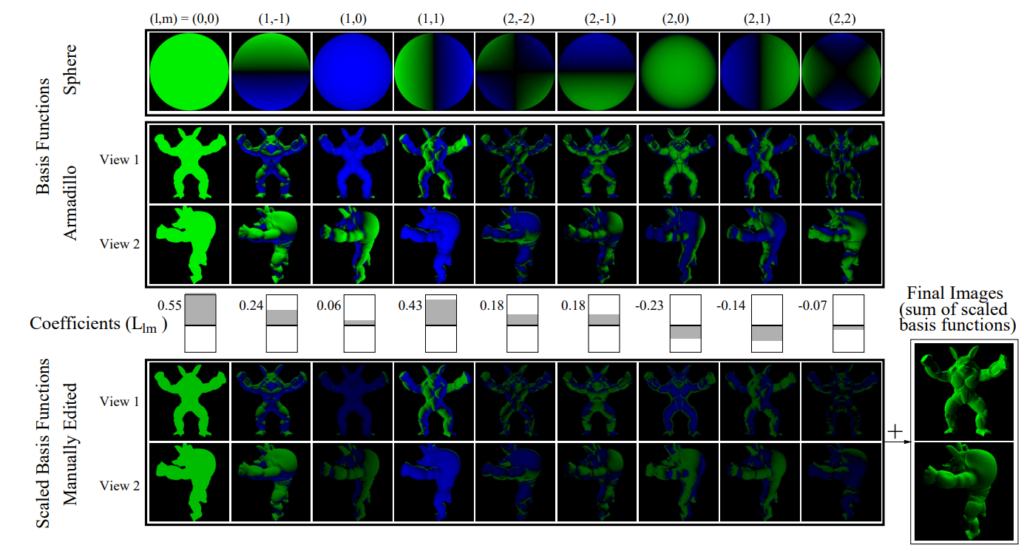
SHは特定の方向に強い分布を持つものであるため、ある意味では特定の方向の代表として働きます。個々に担当する方向の強さはSH係数として表されており、図のようにお互いの方向をカバーするような形でIrradiance全体を作っています。次数$\ell$それぞれの結果は平たく言えば
- $\ell = 0$ は平均(全体)的な色
- $\ell = 1$ はx,y,z軸方向の大まかな色
- $\ell = 2$ は斜め+z方向の詳細な色
となっています。
近似精度
Light ProbeのSH近似はL2までやるのが一般的ですが、L3, L4, …ともっと高い次数まで取って精度を高めてもよさそうなところです。
ですが、これには理由があり、実用上はL2で十分なことが示されています。
$E_{\ell,m}$ の計算においては $\hat{A}_\ell$ が使われていましたが、この $\hat{A}_\ell$ は $\ell > 2$ で極端に値が小さくなることが知られています。具体的な数値としては
$$
\begin{aligned}
\hat{A}_0 &\approx 3.141593 \quad & \hat{A}_1 &\approx 2.094395 \quad \\
\hat{A}_2 &\approx 0.785398 & \hat{A}_3 &= 0 \quad \\
\hat{A}_4 &\approx -0.130900 \quad & \hat{A}_5 &= 0 \quad \\
\hat{A}_6 &\approx 0.049087
\end{aligned}
\tag{10.1}
$$
といった感じです。$\ell = 3$ の係数はもはや0であり、$\ell = 4$ の係数の値は $\ell \le 2$ の係数たちのたった2%しかありません。したがって高次に行けば行くほど $E_{\ell,m}$ は小さくなりやすく、よほど極端な状況(指向性が極端に強い)でない限りはL2で十分なわけです。
実用的な話
理論的な話は終わりにして、ここからは実際の実装について話していきます。
リアルタイムレンダリングでは少しでも計算量を落とすため、定数の計算は事前にまとめた値にしておくことが度々あります。Light Mapでも $1/\pi$ をIrradianceの計算値にまとめておいて、割り算1回分を削減していました。
Light Probeも同様に係数のまとめを行っています。まずはLambert BRDFの $1/\pi$ ですが、これは単純に全体にかかっているので係数であるため、各SH係数に含ませてしまえば問題ありません。
$$
\frac{1}{\pi} E(n) = \sum_{\ell,m} \frac{1}{\pi} E_{\ell,m} Y_{\ell,m}(n) \tag{11.1}
$$
そしてもう1つ行っているのが、SH内部にある定数のまとめです。SHの具体的な関数を見ると正規化項やらで、定数が含まれています。
方向 $\omega$ の座標を $\omega = (x,y,z)$ で表すと、$\ell \le 1$ までのSHは
$$
\begin{align}
Y_{0,0}(\omega) = \frac{1}{2} \sqrt{\frac{1}{\pi}} \\
Y_{1,-1}(\omega) = \sqrt{\frac{3}{4\pi}} y \\
Y_{1,0}(\omega) = \sqrt{\frac{3}{4\pi}} z \\
Y_{1,1}(\omega) = \sqrt{\frac{3}{4\pi}} x \\
\end{align}
\tag{11.2}
$$
という風になっています($\ell = 2$ はAppendixにあるのでご参照ください)。
それぞれにルートがかかった係数がついていることがわかると思います。これをさらに省くためにこれをSH係数の方へとまとめてしまいます。
例えば $\ell = 1, m = -1$ の場合であれば、もろもろをまとめた係数を $\tilde{E}_{\ell,m}$ とすると
$$
\tilde{E}_{1,-1} = \frac{1}{\pi} \sqrt{\frac{3}{4\pi}} E_{1,-1} \tag{11.3}
$$
という形で計算されています。そのため、SHの復元時は $y$ をかけるだけでできるようになっています。
$$
E_{1,-1} Y_{1,-1}(x,y,z) = \tilde{E}_{1,-1} \, y \tag{11.4}
$$
これは他も同様で、それぞれのSHでまとめた結果の係数 $\tilde{E}_{\ell,m}$(Appendix参照)を使うとIrradianceの近似は次のように計算されます。恐らく皆さんが見るSHというのはこういう形式のものだと思います(今後の式と合わせるためちょっとだけ並び替えています)。
$$
\begin{align}
\frac{1}{\pi} E(n) &\approx \tilde{E}_{0,0} \\
&+ \tilde{E}_{1,1} \, x + \tilde{E}_{1,-1} \, y + \tilde{E}_{1,0} \, z \\
&+ \tilde{E}_{2,-2} \, xy + \tilde{E}_{2,-1} \, yz + \tilde{E}_{2,0} \, (3z^2 – 1) \\
&+ \tilde{E}_{2,1} \, xz + \tilde{E}_{2,2} \, (x^2 – y^2) \\
\end{align}
\tag{11.5}
$$
座標系とSH
ここまでの議論はZ-upの右手座標系を前提としてきましたが、他の座標系になればもちろんSHの具体的な式は変化します。例えばY-upの左手座標系であった場合、$z$ と $y$ の役割がひっくり返るので、$y$, $z$ が交換されます。L1,L2であれば、
$$
\begin{align}
Y_{1,-1}(\omega) = \sqrt{\frac{3}{4\pi}} z , \, Y_{1,0}(\omega) = \sqrt{\frac{3}{4\pi}} y , \, Y_{1,1}(\omega) = \sqrt{\frac{3}{4\pi}} x \\
\end{align}
\tag{12.1}
$$
$$
\begin{align}
Y_{2,-2}(\omega) &= \frac{1}{2}\sqrt{\frac{15}{\pi}} xz , \, Y_{2,-1}(\omega) = \frac{1}{2}\sqrt{\frac{15}{\pi}} yz , \, Y_{2,0}(\omega) = \frac{1}{4}\sqrt{\frac{5}{\pi}} (3y^2 -1) \\
Y_{2,1}(\omega) &= \frac{1}{2}\sqrt{\frac{15}{\pi}} xy , \, Y_{2,2}(\omega) = \frac{1}{4}\sqrt{\frac{15}{\pi}} (x^2 – z^2)
\end{align}
\tag{12.2}
$$
となります。
そうなると座標系に応じてSHの計算も変える必要がありそうでなかなか大変そうです。ですが、座標系の違いはSH係数によって吸収でき、SH近似の計算自体はどんな座標系でも(10.5)式で計算可能です。
Y-up座標系におけるSH展開は今までの議論と同様に考えれば、Y-up座標系のSH係数を $\tilde{E}_{\ell,m}’$ として、次のように書くことができます。
$$
\begin{align}
\frac{1}{\pi} E(n) &\approx \tilde{E}_{0,0}’ \\
&+ \tilde{E}_{1,1}’ \, x + \tilde{E}_{1,-1}’ \, z + \tilde{E}_{1,0}’ \, y \\
&+ \tilde{E}_{2,-2}’ \, xz + \tilde{E}_{2,-1}’ \, yz + \tilde{E}_{2,0}’ \, (3y^2 – 1) \\
&+ \tilde{E}_{2,1}’ \, xy + \tilde{E}_{2,2}’ \, (x^2 – z^2) \\
\end{align}
\tag{12.3}
$$
この時、$x^2 + y^2 + z^2 = 1$ であることを用いて変形した上で整理すると、次の式が得られます。
$$
\begin{align}
& \tilde{E}_{0,0}’ + \tilde{E}_{1,1}’ \, x + \tilde{E}_{1,0}’ \, y + \tilde{E}_{1,-1}’ \, z\\
&+ \tilde{E}_{2,1}’ \, xy + \tilde{E}_{2,-1}’ \, yz \, \, – \, \frac{\tilde{E}_{2,0}’ + \tilde{E}_{2,2}’}{2} \, (3z^2 – 1) \\
&+ \tilde{E}_{2,-2}’ \, xz \, \, – \, \frac{3\tilde{E}_{2,0}’ – \tilde{E}_{2,2}’}{2} \, (x^2 – y^2) \\
\end{align}
\tag{12.4}
$$
これは(11.5)式に一致します。つまり、実はSH係数の値が違っていただけで、計算自体は(12.3)式も(11.5)式も全く同じであったわけです。この時のSH係数の関係性は次の表のようになっています。
| Z-up右手系 SH係数 | Y-up左手系 SH係数 | Z-up右手系 SH係数 | Y-up左手系 SH係数 |
|---|---|---|---|
| $\tilde{E}_{0,0}$ | $\tilde{E}_{0,0}’$ | $\tilde{E}_{2,-2}$ | $\tilde{E}_{2,1}’$ |
| $\tilde{E}_{1,-1}$ | $\tilde{E}_{1,0}’$ | $\tilde{E}_{2,-1}$ | $\tilde{E}_{2,-1}’$ |
| $\tilde{E}_{1,0}$ | $\tilde{E}_{1,-1}’$ | $\tilde{E}_{2,0}$ | $-\frac{\tilde{E}_{2,0}’ + \tilde{E}_{2,2}’}{2}$ |
| $\tilde{E}_{1,1}$ | $\tilde{E}_{1,1}’$ | $\tilde{E}_{2,1}$ | $\tilde{E}_{2,-2}’$ |
| $\tilde{E}_{2,2}$ | – $\frac{3\tilde{E}_{2,0}’ – \tilde{E}_{2,2}’}{2}$ |
このように座標系が違っていてもSH係数を適切に変換することでY-up左手座標系のSH展開はZ-up右手座標系のSH展開で計算することができます。これは他のどのような座標系でも同様に変換できます。
任意の座標系から他の座標系に座標を変換する場合、符号の反転と回転の2つの操作で表現することができます。例えば、Z-up右手系からY-up左手系に移すのであれば、X軸に沿って90°回転し、その後Z軸を反転することで作ることができます。
この2つの操作はSH展開において単なるSH係数の変化として現れます。この性質のおかげで任意の座標系のSH展開は(11.5)式で計算できることが保証されています。実際にそうであるのか式で追ってみましょう。
まず符号の反転ですが、これは既に(5.4)式で示されています。任意のSHの符号が反転すれば、それに対応するSH係数も同様に反転します。従って、シンプルに座標系の反転も対応するSH係数の符号反転として現れることになります。
回転については、SHの回転が(6.1)式で示されることから証明できます。関数 $f(\theta,\phi)$ に対するSH展開が与えられていた時、
$$
\small
f_{\ell, m}(\theta,\phi) = f_{0,0} Y_{0,0}(\theta,\phi) + f_{1,-1} Y_{1,-1}(\theta,\phi) + f_{1,0} Y_{1,0}(\theta,\phi) + f_{1,1} Y_{1,1}(\theta,\phi) +… \tag{12.4}
$$
$f(\theta,\phi)$ を回転させて $f(\mathcal{R}(\theta,\phi))$ とした時のSH展開は
$$
\begin{align}
f_{\ell, m}(\mathcal{R}(\theta,\phi)) &= f_{0,0} Y_{0,0}(\mathcal{R}(\theta,\phi)) + f_{1,-1} Y_{1,-1}(\mathcal{R}(\theta,\phi)) \\ &+ f_{1,0} Y_{1,0}(\mathcal{R}(\theta,\phi)) + f_{1,1} Y_{1,1}(\mathcal{R}(\theta,\phi)) +…
\end{align} \tag{12.5}
$$
となります。ここで(6.1)式を代入すると
$$
\begin{align}
f_{\ell, m}(\mathcal{R}(\theta,\phi)) &= 1 \cdot f_{0,0} Y_{0,0}(\theta,\phi) \\
&+ f_{1,-1} \sum_{m’ = -1}^1 D_1^{-1,m’}(\mathcal{R}) Y_{1,m’}(\theta,\phi) \\
&+ f_{1,0} \sum_{m’ = -1}^1 D_1^{0,m’}(\mathcal{R}) Y_{1,m’}(\theta,\phi) \\
&+ f_{1,1} \sum_{m’ = -1}^1 D_1^{1,m’}(\mathcal{R}) Y_{1,m’}(\theta,\phi) + … \tag{12.6}
\end{align}
$$
を得られます。各SHで整理すると次のように式をまとめることができます。
$$
\scriptsize
\begin{align}
f_{\ell, m}(\mathcal{R}(\theta,\phi)) &= 1 \cdot f_{0,0} Y_{0,0}(\theta,\phi) \\
&+ \left\lbrace f_{1,-1} D_1^{-1,-1}(\mathcal{R}) + f_{1,0} D_1^{0,-1}(\mathcal{R}) + f_{1,1} D_1^{1,-1}(\mathcal{R}) \right\rbrace Y_{1,-1}(\theta,\phi) \\
&+ \left\lbrace (f_{1,-1} D_1^{-1, 0}(\mathcal{R}) + f_{1,0} D_1^{0,0}(\mathcal{R}) + f_{1,1} D_1^{1,0}(\mathcal{R}) \right\rbrace Y_{1,0}(\theta,\phi) \\
&+ \left\lbrace f_{1,-1} D_1^{-1,1}(\mathcal{R}) + f_{1,0} D_1^{0,1}(\mathcal{R}) + f_{1,1} D_1^{1,1}(\mathcal{R}) \right\rbrace Y_{1,1}(\theta,\phi) \\
&+ …
\end{align}
\tag{12.7}
$$
式が複雑になりましたが、回転 $\mathcal{R}$ が固定されていれば括弧の中身は定数になります。それぞれのSHにかかる係数部分を $f_{\ell,m}’$ にまとめると次のような形の式が得られます。
$$
\small
f_{\ell, m}(\mathcal{R}(\theta,\phi)) = f_{0,0}’ Y_{0,0}(\theta,\phi) + f_{1,-1}’ Y_{1,-1}(\theta,\phi) + f_{1,0}’ Y_{1,0}(\theta,\phi) + f_{1,1}’ Y_{1,1}(\theta,\phi) +… \tag{12.8}
$$
これは(12.4)式と比較すれば、単にSH係数の値が変化しただけであることが分かります。すなわち、関数の任意の回転はSH係数の変化で吸収できることを示しています。
以上の結果から、座標系の反転、回転に対してSH展開はSH係数の変化という形で対応でき、最終的な計算式としては(11.5)式でOKであることが導けました。これのおかげでランタイム側のIrradiance計算は座標系に依存せずに実装することができます(Unityはどうもそういう実装をしているみたいです)。
(とはいえ、事前計算側は座標系を正しく認識して適切な変換を行う必要があるので、結局実装は煩雑になるとは思います)
UnityのSH
UnityではLight Probeとして内部的にSH近似が使用されており、SkyboxのIrradiance計算などに使用されています。

本当にSHの式が使われているのかを確認するため、Unityの実装を追ってみましょう。Unity(BRP)ではLight Probeからの値は ShadeSH9 という関数によって評価することができます(URPは関数名が違いますが、内部実装は同じ)。
この関数では計算の都合上、normalはshading normal $n = (x,y,z)$ に対して $(x,y,z,1)$ というベクトルを前提としています。
half3 ShadeSH9 (half4 normal)
{
// Linear + constant polynomial terms
half3 res = SHEvalLinearL0L1 (normal);
// Quadratic polynomials
res += SHEvalLinearL2 (normal);
# ifdef UNITY_COLORSPACE_GAMMA
res = LinearToGammaSpace (res);
# endif
return res;
}
最後のやつは単に色の変換(ガンマ補正)なので気にせず、見てみるとL0, L1を計算する SHEvalLinearL0L1 とL2を計算する SHEvalLinearL2 に分かれているようです。それぞれの実装を見るとこんな感じです。
// normal should be normalized, w=1.0
half3 SHEvalLinearL0L1 (half4 normal)
{
half3 x;
// Linear (L1) + constant (L0) polynomial terms
x.r = dot(unity_SHAr,normal);
x.g = dot(unity_SHAg,normal);
x.b = dot(unity_SHAb,normal);
return x;
}
// normal should be normalized, w=1.0
half3 SHEvalLinearL2 (half4 normal)
{
half3 x1, x2;
// 4 of the quadratic (L2) polynomials
half4 vB = normal.xyzz * normal.yzzx;
x1.r = dot(unity_SHBr,vB);
x1.g = dot(unity_SHBg,vB);
x1.b = dot(unity_SHBb,vB);
// Final (5th) quadratic (L2) polynomial
half vC = normal.x*normal.x - normal.y*normal.y;
x2 = unity_SHC.rgb * vC;
return x1 + x2;
}
以下の点を念頭に置いてこの式を展開すると、これは正しく式(10.5)に一致します。
unity_SH~という変数がSH係数を表している- RGBそれぞれの値は
unity_SH~のRGBに格納されている(unity_SHCだけ例外) - Z-up座標系のSHを使用している(「座標系とSH」を参照)
それぞれの式を一つ一つ紐解いて、本当に一致するか見ていきましょう。
L0,L1の評価部分を見るとnormalとunity_SHAの内積を取っています。ここで渡されるnormalのw成分は1.0であることを思い出し、unity_SHA を $(\mathrm{SHA_x, SHA_y, SHA_z, SHA_w})$ と定義すれば
$$
\mathrm{SHA_x} \, x + \mathrm{SHA_y} \, y + \mathrm{SHA_z} \, z + \mathrm{SHA_w} \tag{13.1}
$$
を計算しているわけです。(11.5)式と見比べればSHAのx,y,z成分は $\tilde{E}_{1,1},\tilde{E}_{1,0} \tilde{E}_{1,-1}$ に相当し、wは $\tilde{E}_{0,0}$ であることが分かります。内積でわかりにくくなっていますが、L0とL1をちゃんと計算していることが確認できます。
half4 vB = normal.xyzz * normal.yzzx;
x1.r = dot(unity_SHBr,vB);
x1.g = dot(unity_SHBg,vB);
x1.b = dot(unity_SHBb,vB);
L2の計算部分を見てみると vB に変数をまとめています。vB の中身を追ってみると $(xy,yz, z^2,xz)$ であることがわかり、
$$
\mathrm{SHB_x} \, xy + \mathrm{SHB_y} \, yz + \mathrm{SHB_z} \, z^2 + \mathrm{SHB_w} xz \tag{13.2}
$$
という式を計算していることになります。すなわち、SHBの中身は $(\tilde{E}_{2,-2},\tilde{E}_{2,-1}, \tilde{E}_{2,0}, \tilde{E}_{2,1})$ というSH係数を保持していることが推測できます。
ただ3つ目の式に問題があり、SHの定義に従えば本来 $3z^2 – 1$ とすべきとこなのですが、$z^2$ で計算しています。恐らくですが $-1$ という部分は展開すればただの定数なので、L0の係数に突っ込んでいるのではないかと思います。
多分、実は $\tilde{E}_{0,0}$ は正しくは $\tilde{E}_{0,0} \rightarrow \tilde{E}_{0,0} – \tilde{E}_{2,0} / 3$ ではないかなと考えています(本当のことを知っている方がいたら教えてください)。
half vC = normal.x*normal.x - normal.y*normal.y;
x2 = unity_SHC.rgb * vC;
$\ell = 2$ の項は $m = 2$ だけまだ計算できていないので最後 unity_SHC を使って評価をしています。この変数だけ若干今の流れとは違って、RGBの $\tilde{E}_{2,2}$ をそれぞれrgbに入れています。
$$
\mathrm{SHC} \, (x^2 – y^2) \tag{13.3}
$$
各式の結果を加算すれば、最終的に(11.5)式を評価していることになります。Unityの謎の式はIrradianceをSH近似した結果を計算していた、ということが分かったかと思います。
終わりに
非常に長い記事を見て頂いてありがとうございました。
SHは一般式が複雑だったり、ややこしい事情があるせいで少々学習が難しいと感じます(私も初学者のころはかなり苦戦しました)。しかし、1回やってみると中々に面白く、意外とシンプルに取り扱うことができると分かりました。特にIrradianceの近似は画像の圧縮にも通じていて、SHをうまく使ったエレガントな手法であると感銘を受けました。
今回の記事はそこを伝えるつもりで書きました。この記事を通してSHの面白さが伝われば幸いです。
まだまだSHに関する面白いトピックはあるため、今後余裕があればまた続きを書いていこうと思います。
Appendix
実SH
$\ell = 0$
$$
Y_{0,0} = \frac{1}{2} \sqrt{\frac{1}{\pi}}
$$
$\ell = 1$
$$
\begin{align}
Y_{1,-1}(x,y,z) &= \sqrt{\frac{3}{4\pi}} y \\
Y_{1,0}(x,y,z) &= \sqrt{\frac{3}{4\pi}} z \\
Y_{1,1}(x,y,z) &= \sqrt{\frac{3}{4\pi}} x \\
\end{align}
$$
$\ell = 2$
$$
\begin{align}
Y_{2,-2}(x,y,z) &=\frac{1}{2}\sqrt{\frac{15}{\pi}} xy \\
Y_{2,-1}(x,y,z) &=\frac{1}{2}\sqrt{\frac{15}{\pi}} yz \\
Y_{2,0}(x,y,z) &=\frac{1}{4}\sqrt{\frac{5}{\pi}} (3z^2 -1) \\
Y_{2,1}(x,y,z) &=\frac{1}{2}\sqrt{\frac{15}{\pi}} xz \\
Y_{2,2}(x,y,z) &=\frac{1}{4}\sqrt{\frac{15}{\pi}} (x^2 – y^2) \\
\end{align}
$$
$\hat{A}_\ell$の解析解
$$
\begin{aligned}
&l = 1 \quad && \hat{A}_1 = \frac{2\pi}{3} \\
&l > 1,\ \text{odd} \quad && \hat{A}_l = 0 \\
&l\ \text{even} \quad && \hat{A}_l = 2\pi \frac{(-1)^{\frac{l}{2}-1}}{(l+2)(l-1)}
\left[ \frac{l!}{2^l \left( \left( \frac{l}{2} \right)! \right)^2} \right]
\end{aligned}
$$
SH係数計算
Light Probeに使われているベイク結果の各係数(プラットフォームによると思うのであくまで一例程度に)
$\ell = 0$
$$
\tilde{E}_{0,0} = \frac{1}{2 \pi} \sqrt{\frac{1}{\pi}} E_{0,0}
$$
$\ell = 1$
$$
\begin{align}
\tilde{E}_{1,-1}&= \frac{1}{\pi} \sqrt{\frac{3}{4\pi}} E_{1,-1} \\
\tilde{E}_{1,0} &= \frac{1}{\pi} \sqrt{\frac{3}{4\pi}} E_{1,0}\\
\tilde{E}_{1,1} &= \frac{1}{\pi} \sqrt{\frac{3}{4\pi}} E_{1,1}\\
\end{align}
$$
$\ell = 2$
$$
\begin{align}
\tilde{E}_{2,-2} &=\frac{1}{2 \pi}\sqrt{\frac{15}{\pi}} E_{2,-2} \\
\tilde{E}_{2,-1} &=\frac{1}{2 \pi}\sqrt{\frac{15}{\pi}} E_{2,-1} \\
\tilde{E}_{2,0} &=\frac{1}{4 \pi}\sqrt{\frac{5}{\pi}} E_{2,0} \\
\tilde{E}_{2,1} &=\frac{1}{2 \pi}\sqrt{\frac{15}{\pi}} E_{2,1} \\
\tilde{E}_{2,2} &=\frac{1}{4 \pi}\sqrt{\frac{15}{\pi}} E_{2,2} \\
\end{align}
$$
Unity実装への推測
実行時における$\ell = 2, m = 2$の計算量を減らすため、一部L0にL2の定数値を含ませている可能性がある。恐らく次のような値を計算していると考えられる
$$
\begin{align}
\tilde{E}_{0,0} &= \frac{1}{2 \pi} \sqrt{\frac{1}{\pi}} E_{0,0} \, – \, \frac{1}{4 \pi}\sqrt{\frac{5}{\pi}}E_{2,0} \\
\tilde{E}_{2,0} &= \frac{3}{4 \pi}\sqrt{\frac{5}{\pi}} E_{2,0} \\
\end{align}
$$
Reference
- Wikipedia, Spherical harmonics, https://en.wikipedia.org/wiki/Spherical_harmonics
- [Ramamoorthi, Hanrahan. 2001] On the relationship between radiance and irradiance: determining the illumination from images of a convex Lambertian object, https://graphics.stanford.edu/papers/invlamb/
- [Ramamoorthi, Hanrahan. 2002] An Efficient Representation for Irradiance Environment Maps, https://graphics.stanford.edu/papers/envmap/
- [Roughton, et al. 2024] ZH3: Quadratic Zonal Harmonics, https://dl.acm.org/doi/10.1145/3651294
- 完全に任意ではなく、目的の関数が自乗可積分関数であることが要請されます。 ↩︎
- ラプラス方程式の性質から来ている…らしいです ↩︎
- おそらく元々は説明のようにDynamicなオブジェクトに対するDiffuse反射を目的とされていたと思うのですが、近年ではLight Mapの代わりにLight Probeを使うという動きもみられます(Light Mapも無駄な容量が多かったりと難しい面がある & Light ProbeがGI計算に使えるなどの理由) ↩︎



