ポリゴンリダクション事始め

応用技術部の尾崎と申します。社内では主に、ジオメトリ処理および、点群処理に関わっています。今回はポリゴンリダクションについて概説をと、「無茶ぶり」を頂きましたので記事を書いていきたいと思います。何故、無茶ぶり、などと嫌味をいうのか？というのは、おいおい記事の中で。

本記事は、CGに関するワードくらいは知ってるけれど、プログラミングの事は良く分かってないアーティストからエンジニアとして働いておられる方まで、ポリゴンリダクションがどのように行われるのか？基本的な知識をお持ちでない人を対象に進めていきたいと思います。多少冗長に感じられるかと思いますが、ご容赦ください。

ポリゴンリダクションとは？

LOD（Level of Details）という言葉になじみのある方、ない方、様々かと思いますが、CGやゲームの世界ではとても重要な言葉です。図１のスタンフォードバニーは、10万ポリゴンにも満たないポリゴンで表現された形状ですが、昨今のゲームや映画では、登場キャラクタの顔だけで数百万、数千万というポリゴン数で表される事も珍しくありません。それこそ皺までポリゴンで表現することで豊かな表現力を備えた形状になりますが、この巨大なといっていいサイズの形状がゲームや映画の全ての場面で必要になるでしょうか？表情がアップになった場面では必要でしょう、ですがキャラクタが100mもカメラから離れた場面では、どうでしょうか？描画領域で100×100ピクセルに収まるようなキャラクタに、数千万ポリゴンが必要でしょうか？場面によって、同じキャラクタでも描画に利用する形状を変えたいという要求にこたえるもの、それがLevel of Detailsの考え方です。LODは描画に限らず、ポリゴン数に比例して計算リソースを消費する様々な用途で必要とされます。ポリゴンリダクションとは、形状を表現するポリゴン数を減らす事を目的とした、形状のLODを提供する一つの手段ということです。

ポリゴンを削減する方法とは？

ここではポリゴンを削減する方法について考えてみましょう。図2は、弊社で開発をしているポリゴンリダクションツールで、図１の形状を17000ポリゴン（オリジナルは約70000ポリゴン程）程度までポリゴン数を削減した結果です。ポリゴンリダクションでは、ポリゴンをむやみに減らせばいいのではなく、図の様に元の形状の特徴を可能な限り保ったまま、処理の際に計算リソースを奪うポリゴン数を減らしたいという目的で行われます。しかしながら、ポリゴン数を減らす方法も唯一無二ではなく、様々な方法が存在します。近隣の複数頂点を一点に纏める、形状を曲面関数の集合で表現し曲面を低ポリゴンで表現する、辺を縮退する、円柱や立方体などプリミティブな形状で抽象化する、形状のシルエットを波形で表現しノイズリダクションする、などなど。この記事で、そのすべてを網羅することなど到底できませんし、また皆さんにお付き合いいただくのも無理と言うものです。故に、また無茶（略

この記事では、その中の一つであるEdge-Collapse-Based-Mesh-Simplification、辺の縮退を基本的な考え方として採用したポリゴンリダクションについて概説します。やっと、前置き終了です。（日本語では、あるいはゲーム業界では、ポリゴンリダクションという事が多いですが、研究者はMesh Simplification, Mesh Decimationなどという事が多いです。）

辺の縮退とは？

辺を縮退させると言われて、その挙動がイメージできる方も、そうでない方もおられるでしょうということで、ここでは辺の縮退について、もっと言えば良い辺の縮退について、考えてみます。

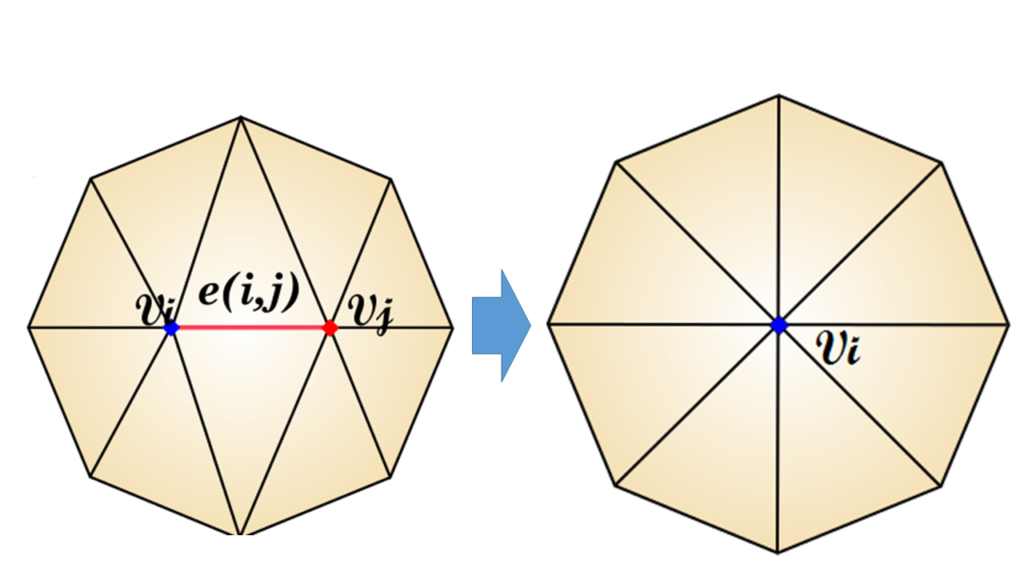
図3に示したのは、辺の縮退の様子です。頂点ViとVjからなるエッジe(i,j)がなくなって、エッジの両側に存在する三角形が消え、二つの頂点は新たに頂点Viに統合される事で、2つの三角形が削減されています。1回の辺の縮退によって2ポリゴンまたは1ポリゴン減りますので、これを何百回、何千回と繰り返す事で、ポリゴンリダクションを実現しましょう、というのが辺の縮退を基本的な考え方としたポリゴンリダクションです。2ポリゴン以上が消えるようなケースは、非多様体あるいは二多様体と言われ、正常な処理を行えない場所になります。（もちろん回避手段はあります）

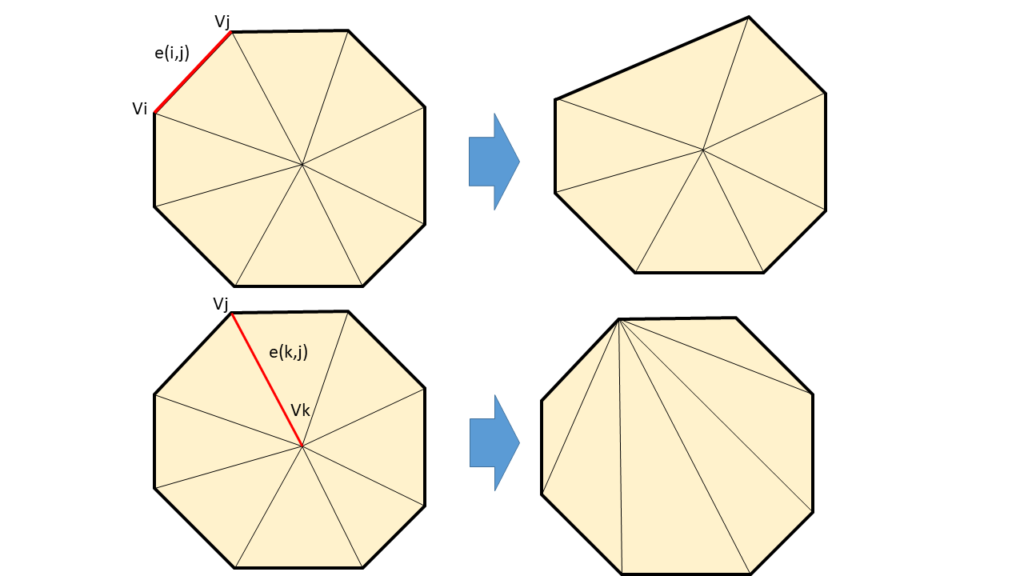
図４に、縮退の例を2例提示しました。e(i,j) の縮退、e(k,j)の縮退、どちらがより良い縮退でしょうか？答えは、場合による・・・って言ってしまうと終わりなので、ここでは、元の形状の輪郭を損なわないという条件を、良い縮退と定義します。（この良い縮退の定義が大事なので、自明に思えるこのケースでも敢えて強調しますが、本当に場合によるのです。）輪郭を損なってないのは、e(k,j)であることは一目瞭然です。では、なぜでしょう？輪郭を損なわないという良い縮退の定義を、もう少しだけ論理的に表現してみましょう。図4の上段、下段では何が変化しているでしょうか？そう、縮退後の面積です。

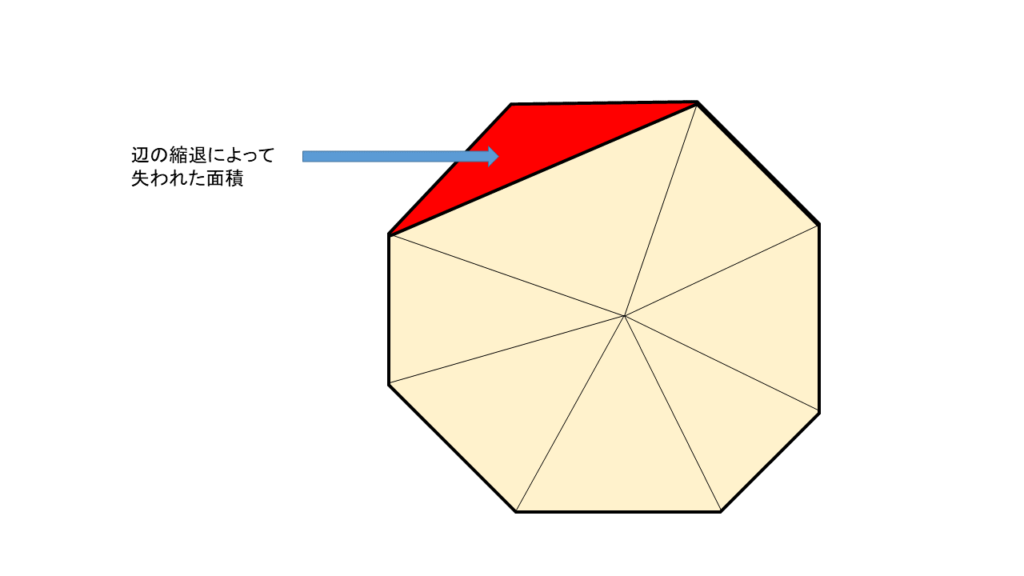
図5を見てください。図４のe(i,j)に縮退によって失われた面積を赤く表示しました。辺の縮退によって、元の図形が失った面積をエッジの縮退のコストと定義します。e(k,j)では、このコストはゼロですね。平面図形の輪郭を保ちたい場合には、辺の縮退による面積の変化量をコストとして支払うポリゴンリダクションを行えばいい、という事が言えると思います。実際、このような考え方を部分的に取り入れている研究もあります。（P. Lindstrom and G. Turk, “Fast and Memory Efficient Polygonal Simplification,” Proc. Visualization ’98, IEEE Computer Soc. Press, Oct. 1998, pp. 279–286)

3次元形状における良い辺の縮退とは？

場合による・・・で終わってはしょうがないので、前段で説明した面積を保つということをベースにして考えてみましょう。数学では、1次元から初めて、次元を一つづつあげて行って、やがてN次元でも成立すると証明するようなことをよくやりますね。同じように、面積から1次元あげて考えてみましょう、面積を1次元あげれば体積です。つまり、三次元の縮退において特徴を保つための一つの良い指針は、体積の変化量を追えばいいのだという事になります。

では、体積はどのように求めればいいのでしょうか？任意の形状のある範囲の限定的な体積の計算はどのように求めますか？三角錐や球で形状を埋めて、その総和で近似しますか？とても時間がかかりそうです。直観的に考えても、体積を求めるのは、現実的な手法とは言えません。しかし、体積そのものを求めるのは難しくても、体積に比例して、なおかつもっと簡単に求められるものを用いればどうでしょうか？ここで、体積とは何だったのか？思い出してみましょう。学校で習った体積の計算方法は、底面積×高さだったはずです。あるいは、よりイメージしやすいのは面積を高さ方向に積分したものかもしれません。

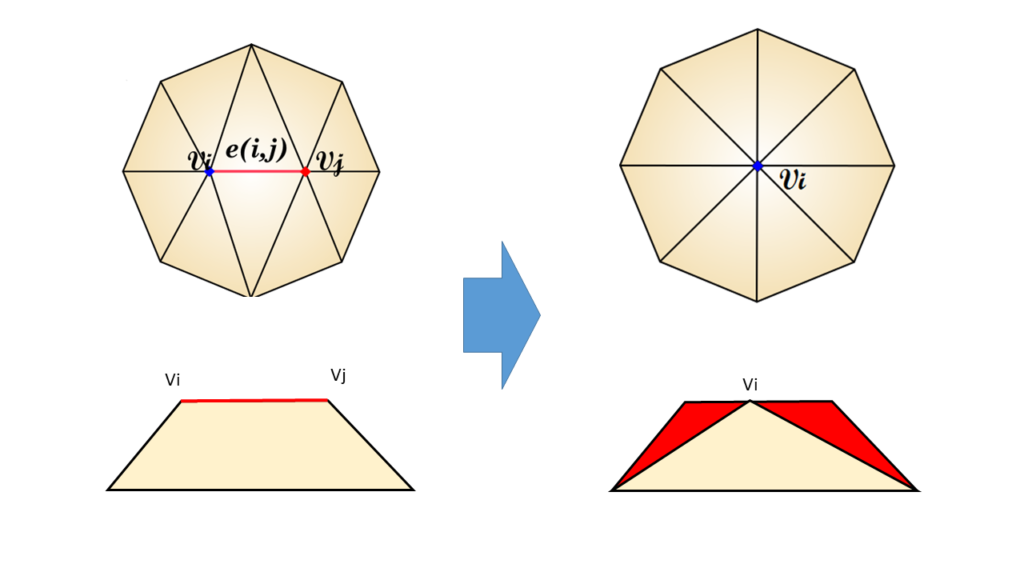
図３の辺の縮退を三次元化してみましょう。図6では、図3を上から見たものとみなして、それを横から見た状態を並べています。真上から見た場合は総面積が変化していませんが、横から見た場合の面積は大きく変化しています。つまり、3次元空間上では体積が変化している事になります。赤い部分の体積の変化量を計算するのは、さほど難しくもないのですが、それでも数万回繰り返すことを考えると適切とは言えないでしょうし、実際の形状はもっと構成も複雑で、底面が同じ高さに並んでるなんてことも殆どありませんから、計算コストは高くなります。ですので、さきほど述べたように、体積に比例する高さを考えるのが良さそうです。

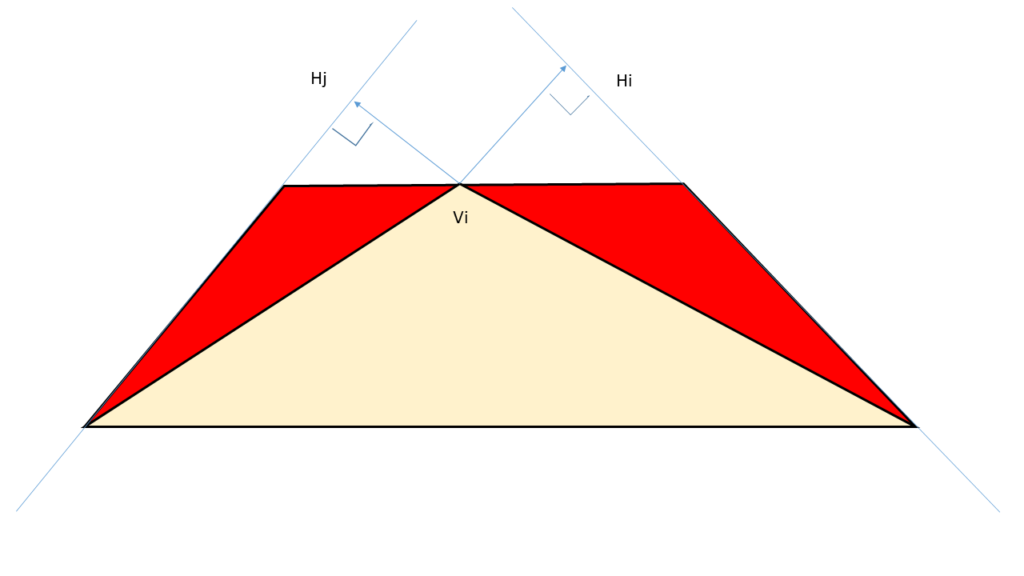
この場合、変化した量に比例する高さとは、どのように求められるものでしょうか？それを図７にしめしました。頂点viと、元の平面Hi、Hjとの距離を考えればいいのです。この距離が遠くなるほど必然的に体積の変化量は大きくなることは直感的に理解できると思います。この考え方を用いた手法こそが、この記事で解説したかった、Qadric Error Metricです。（Michael Garland and Paul S. Heckbert. Surface simplication using quadric error metrics. In Proc. SIGGRAPH ’97, pp. 209{216. ACM Press/Addison-Wesley Publishing Co., New York, NY, USA, 1997.）

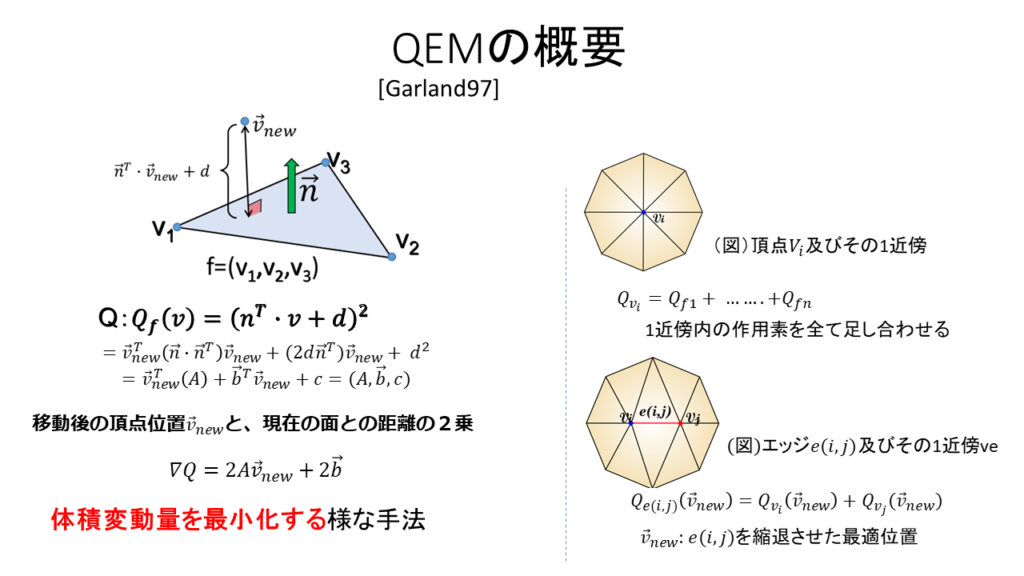
Quadric Error Metric

図8をご覧ください、ここまでの説明で直感的にご理解いただけてればもう充分です。式についてはあえて詳しくは説明しませんし、研究の概要についても詳説はしません。それをやってしまうと、このブログの終わりが見えなくなってしまうので（笑）乱暴に言ってしまうと、ここまで直感的なたとえ話で説明した事象を定式化したもので、各ポリゴンについて縮退後の頂点位置によらず、元のポリゴンの情報だけで表現できる作用素Quadricsが求められるという事です。ただし、この作用素は面毎に求められるので、ある辺が縮退する場合の作用素は、辺の両端にある頂点を使っている全ての面に対する作用素の総和になるという事です。この両端の作用素によって任意の頂点位置に対する辺の縮退コストを計算することが出来ます。乱暴にまとめましたが、これだけです。

終わりに

あとは、この作用素の計算と辺の縮退を繰り返して、もっともコストの低い辺を繰り返し縮退させていけば簡略化を終えることが出来ます。しかし、実際の形状には、テクスチャも適用されていますし、ものによってはスキンアニメーションをしたりしますし、色が適用されているかもしれません、形状も高さを求めにくい建物のような平面の多い角ばった形状かもしれません、求める結果は形状の維持ではなく、仕上がったLODの面の面積の一様さかもしれません。テクスチャを張った時に綺麗に見える事かもしれません。アニメーションさせてみても壊れない事かもしれません。入力は、何十億ポリゴンもあるような巨大な形状かもしれません。点群の集合で表現されているかもしれません。複雑に入り組んだマテリアル設定がなされてるかもしれません。コストの計算方法には、その求める結果、入力となる形状の特徴に応じただけのパターンが存在します。図9にみられるように、何を大事にしたか、どんな概念で最適化式をモデル化したかで、その結果は大きく変える事ができます。

このブログ記事で、ご紹介した方法は、あくまで、その中の一つに過ぎないのです。自分たちが、お客様が、何を求めているのか？を考え、最良の結果に合わせて最適な計算方法をみつけること、それが弊社が考える研究開発であると思います。また私たちが既存の製品に満足せず新たな挑戦を続ける理由でもあります。この記事が、皆様にとっての良い答えを探す旅の一助となりましたら、無茶ぶりに答えて長すぎる記事を書いた甲斐があるというものです！

私の拙い説明にお付き合いいただきありがとうございました。