Unity6 + URP で動くパストレーサーを実装してみよう Part3
はじめに
こんにちは。シリコンスタジオ 研究開発室の川口です。
前回、前々回で URP 相当のライティングが動作するレイトレーシングを実装しました。
今回はその続きとしてついにパストレーサーを実装していきます。
一連の記事ではパストレーシングのアルゴリズムを全て自力で実装するわけではありません。
極力 Unity と URP の機能に頼りながら実装してくことで必要な処理やその流れを把握して、パストレーシング全体のアルゴリズムをざっくりと俯瞰的に理解することを目指します。
対象読者:Unity、URP に触ったことのある方・GPU レイトレーシングの実装に興味のある方
Unity6 + URP で動くパストレーサーを実装してみよう Part 3
さっそく実装していきます。
実装は前回の内容をそのまま引き継いでいます。
執筆時点の環境(2025年2月)
- Unity 6 (6000.0.27f1)
- URP 17.0.3
乱数の実装
まずパストレーシングには確率的なサンプリングが必要なのでそのための乱数生成器を用意しましょう。
シェーダには乱数を生成する機能は用意されていないので自分で疑似乱数生成器を実装する必要があります。
Shadertoy などでは sin 関数を使った方法がよく使われていますが品質は良くないと言われています。
GPU で行うパストレーシングで使う乱数には、暗号的な強度は必要ありませんが、長い周期・シードに対する無相関性・複雑すぎない処理(高速な動作)は欲しいところです。
また、4次元入力2次元出力の乱数生成器がシンプルなパストレーサーにはよくマッチします。
(スクリーン座標2次元+サンプルインデックス1次元+サンプル次数1次元(=4次元)のシードを入力に、乱数のペア(=2次元)が得られる)
乱数の品質についての詳しい議論は(私もあまり理解していないので)他を参照してください。
ちょうど最近とても素晴らしい記事を投稿されている方がいらっしゃいました。
高速で頑健なシェーダー乱数の比較と提案
今回はこの方の提案した方法ではなく、Hash functions for gpu rendering [Jarzynski 2020] で提案されている PCG4D というアルゴリズムを使います。
Random.hlsl ファイルを作ってそこに RNG (Random Number Generator)構造体を実装します。
ピクセル座標とサンプルインデックスと次数を入力して rand() で4次元の乱数を取得できます。
この実装は4次元入力4次元出力ですが使うときに2次元ペア2個のように使えば用途にマッチしています。
struct RNG
{
uint4 seed;
float uintTofloat(uint x)
{
return asfloat(0x3f800000u | (x >> 9u)) - 1.0f;
}
uint4 pcg4d(uint4 v)
{
v = v * 1664525u + 1013904223u;
v.x += v.y * v.w; v.y += v.z * v.x;
v.z += v.x * v.y; v.w += v.y * v.z;
v.x = v.x ^ (v.x >> 16u); v.y = v.y ^ (v.y >> 16u);
v.z = v.z ^ (v.z >> 16u); v.w = v.w ^ (v.w >> 16u);
v.x += v.y * v.w; v.y += v.z * v.x;
v.z += v.x * v.y; v.w += v.y * v.z;
return v;
}
void init(uint2 pixelCoords, uint sampleIndex, uint dim)
{
//< Seed for PCG uses a sequential sample number in 4th channel,
// which increments on every RNG call and starts from 0
seed = uint4(pixelCoords.x, pixelCoords.y, sampleIndex, dim);
}
float4 rand()
{
seed.w++;
uint4 v = pcg4d(seed);
return float4(uintTofloat(v.x), uintTofloat(v.y), uintTofloat(v.z), uintTofloat(v.w));
}
};
Random.hlsl を MyPathTracingShader.raytrace でインクルードしておきましょう。
#include "Random.hlsl"
ちなみに uint4 で保持している内部シードの .w 要素は乱数の現在の次数を示していて、rand() を呼ぶ度に次数が進みます。
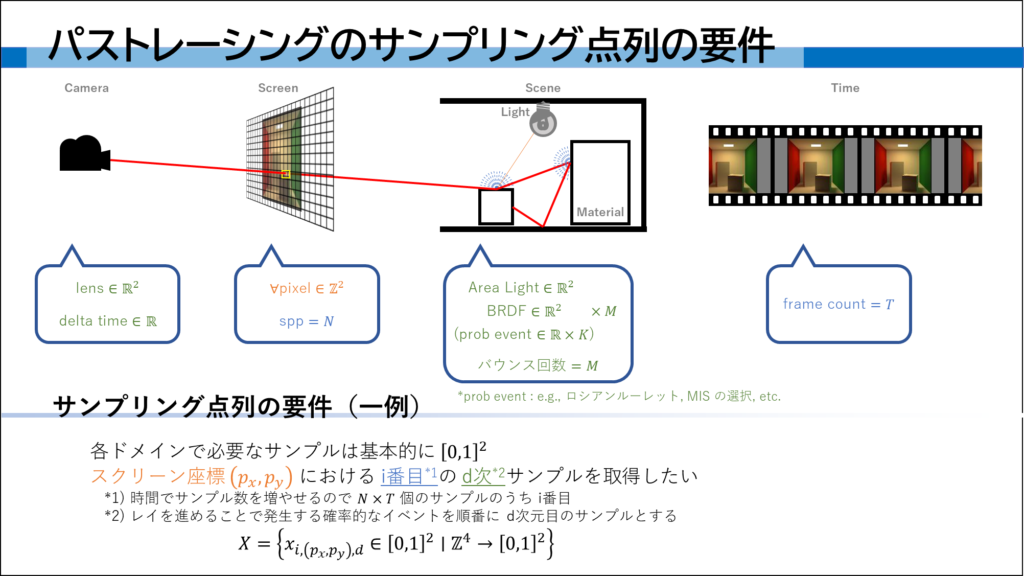
パストレーシングにおける乱数の次数は、乱数を要求するイベント(ドメイン)に対応しています。
例えば、レンズのサンプリングが 0,1 次の乱数ペア、光源のサンプリングが 2,3 次、BRDF のサンプリングが 4,5 次というようにドメインが次数に対応していきます。
(今の実装は1次ごとに4つの乱数を得ていますがいいように読み替えてください。)
パストレーシングロジックの実装
さて、これでやっとパストレーシングを実装出来ます。
レンダリング方程式
パストレーシングはレンダリング方程式の数値解法の一種です。
今回は次のようなレンダリング方程式をモンテカルロ積分という方法で解くことで、各ピクセルの輝度(色)を求めます。
$$ L_o(\boldsymbol{x}, \boldsymbol{\omega}_o) = L_e(\boldsymbol{x}, \boldsymbol{\omega}_o) + \int_\Omega {f(\boldsymbol{x}, \boldsymbol{\omega}_i, \boldsymbol{\omega}_o) L_i(\boldsymbol{x}, \boldsymbol{\omega}_i) | \boldsymbol{\omega}_i \cdot \boldsymbol{n} | d\boldsymbol{\omega}_i} $$
各記号の説明はいったん置いておきます。
これだけ見ると難しいですが、一度簡単に整理して実装に落とし込むことでかなり理解しやすくなると思います。
まず積分のままではコードに落とし込めないので数値解法としてモンテカルロ積分で近似します。
$$ L_o(\boldsymbol{x}, \boldsymbol{\omega}_o) = L_e(\boldsymbol{x}, \boldsymbol{\omega}_o) + \frac{1}{N} \sum_i^N \frac{f(\boldsymbol{x}, \boldsymbol{\omega}_i, \boldsymbol{\omega}_o) L_i(\boldsymbol{x}, \boldsymbol{\omega}_i) | \boldsymbol{\omega}_i \cdot \boldsymbol{n} |}{p(\boldsymbol{\omega}_i)} $$
何か増えている記号もありますが、単に積分を総和に置き換えているだけです。
ここで確率的なサンプリングという概念が発生しているのですが、実装するときに考えましょう。
この式における総和はパストレーシングにおけるサンプリングを表していて、1ピクセルあたりにたくさん($N$ 本)のレイを飛ばしてその結果の平均を取る操作と対応します。
今は完全にリアルタイムで動作するパストレーサーの作成を目指しているわけではありませんが、ゲームエンジン上で動かすということで1フレームあたりの計算量は極力減らしたいです。
1フレームあたり1本のレイだけ飛ばす(1 spp : samples per pixel)とすると、総和も式から取り除けます。
たくさんのサンプルの平均を取る処理自体は必要なので、後で複数フレームに渡った処理として実装します。
$$ L_o(\boldsymbol{x}, \boldsymbol{\omega}_o) = L_e(\boldsymbol{x}, \boldsymbol{\omega}_o) + \frac{f(\boldsymbol{x}, \boldsymbol{\omega}_i, \boldsymbol{\omega}_o) L_i(\boldsymbol{x}, \boldsymbol{\omega}_i) | \boldsymbol{\omega}_i \cdot \boldsymbol{n} |}{p(\boldsymbol{\omega}_i)} $$
だいぶ式がスッキリしたところで各記号を説明します。
- $\boldsymbol{x}$ : 式を評価する点(レイがヒットした位置)の座標。
- $\boldsymbol{n}$ : 式を評価する点(レイがヒットした位置)の法線。
- $\boldsymbol{\omega}_o$ : 光の出射方向ベクトル。カメラから飛ばした最初のレイであれば、ヒット位置から視点への方向ベクトル。
- $\boldsymbol{\omega}_i$ : 光の入射方向ベクトル。この確率的な選び方がパストレーシング(モンテカルロ積分)において非常に重要。
- $L_o(\boldsymbol{x}, \boldsymbol{\omega}_o)$ : 点 $\boldsymbol{x}$ から $\boldsymbol{\omega}_o$ 方向へ出射する放射輝度。カメラから飛ばした最初のレイであれば、これがピクセルの色になる。
- $L_e(\boldsymbol{x}, \boldsymbol{\omega}_o)$ : 点 $\boldsymbol{x}$ から $\boldsymbol{\omega}_o$ 方向へ発光する放射輝度。
- $L_i(\boldsymbol{x}, \boldsymbol{\omega}_i)$ : $\boldsymbol{\omega}_i$ 方向から点 $\boldsymbol{x}$ へ入射する放射輝度。
- $f(\boldsymbol{x}, \boldsymbol{\omega}_i, \boldsymbol{\omega}_o)$ : 点 $\boldsymbol{x}$ 表面上における BRDF(材質の反射特性)。
- $p(\boldsymbol{\omega}_i)$ : $\boldsymbol{\omega}_i$ を確率的に選ぶときに使う確率密度関数。
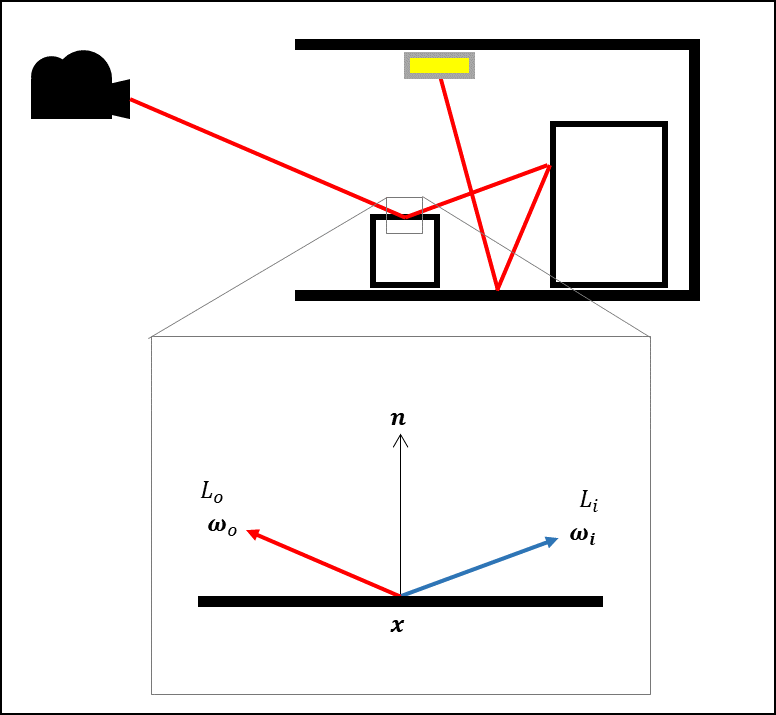
パストレーシングはカメラから光源へのパスを繋ぐ計算なので、計算が光の向きとは逆方向($\boldsymbol{\omega}_o$ から $\boldsymbol{\omega}_i$)になることに注意してください。
($o$ は光が outgoingする方向、$i$ は光が incomingしてくる方向を表すサブスクリプトです)
文献や実装によってこの $o$ と $i$ は逆に記述されることもあるので、カメラと光どちらが基準になっているのか文脈からしっかり理解する必要があります。
さてここで重要なのは、(カメラからのレイの反射を辿っているとき)$L_i(\boldsymbol{x}, \boldsymbol{\omega}_i)$ は次の反射において $L_o(\boldsymbol{x}, \boldsymbol{\omega}_o)$ になるということです。
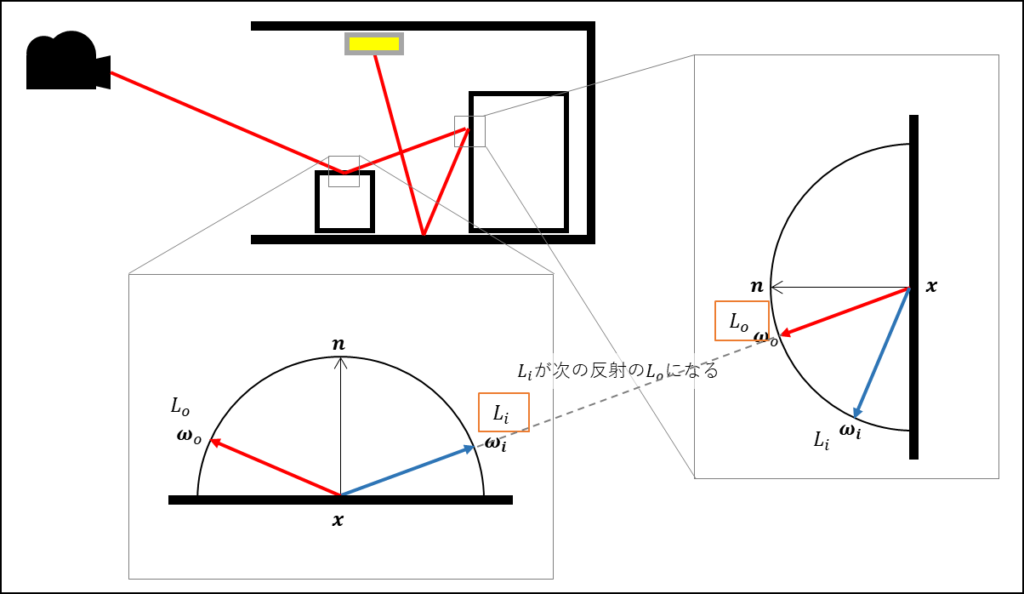
つまり $L_i(\boldsymbol{x}, \boldsymbol{\omega})$ の式は入れ子(再帰)の形になって表現することができます。
パストレーシングにおける複数回の反射はこの式に対応します。
(反射回数を $i$, $o$ に対応させて表記しています。)
$$ L_0(\boldsymbol{x}_0, \boldsymbol{\omega}_0) = \frac{f(\boldsymbol{x}_0, \boldsymbol{\omega}_1, \boldsymbol{\omega}_0) | \boldsymbol{\omega}_0 \cdot \boldsymbol{n}_0 |}{p(\boldsymbol{\omega}_0)} \left( \frac{f(\boldsymbol{x}_1, \boldsymbol{\omega}_2, \boldsymbol{\omega}_1) | \boldsymbol{\omega}_1 \cdot \boldsymbol{n}_1 |}{p(\boldsymbol{\omega}_1)} \left( \dots \right) \right) $$
($L_e$ は省略)
再帰は無限に展開できるので何かしらで打ち切る必要があります。
パストレーシングではロシアンルーレットという確率的な方法がよく使われますが、今回は簡単にするため定数回もしくは $L_e$ が非ゼロ、つまりレイが発光面に当たった時点(もしくは何にも当たらず空へ飛んで行ったら)で打ちきりとします。
$$ L_0(\boldsymbol{x}_0, \boldsymbol{\omega}_0) = \frac{f(\boldsymbol{x}_0, \boldsymbol{\omega}_1, \boldsymbol{\omega}_0) | \boldsymbol{\omega}_0 \cdot \boldsymbol{n}_0 |}{p(\boldsymbol{\omega}_0)} \left( \dots \left( L_e(\boldsymbol{x}_N, \boldsymbol{\omega}_{N}) \right) \right) $$
$L_0$ とカメラの間でセンサー(カメラのレンズなど)の特性を評価することも多いですが、今回は $L_0$ がそのままピクセルの色になります(レイトレ外の URP のポストエフェクトなどはかかります)。
この式を画面の全てのピクセルごとに計算することでレンダリングされた絵ができます。
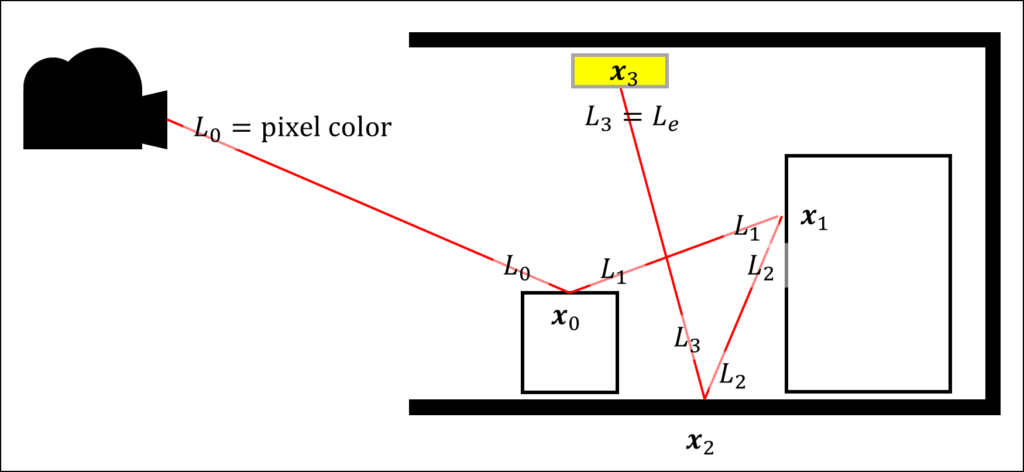
さて、レイトレーシングにおいて光源とは発光 $L_e$ がある表面を指します。
この値は PBR マテリアルにおける Emission (Emissive) の値に対応します。
この Emission はゲームエンジンのようなリアルタイムのレンダラーにおいては基本的に光源として扱われません(ベイクが必要)。
一方でゲームエンジンで使われる光源は、ディレクショナルライト、ポイントライト、スポットライトのような専用のライトオブジェクトです。
これは面積を持たない数値的な表現であり、レイが当たることがないため上記の式では評価されません。
前回実装した MyUniversalFragmentPBR は、レイトレの中でレイが当たることのないそれらのライトを評価する処理です。
このパストレーシングにおいて、MyUniversalFragmentPBR で評価される直接光の輝度は、各反射点を評価するときの $L_e$ の値と同じように扱うことでゲームのライティングをパストレーサーに組み込むことができます。
ただし再帰打ち切りの条件はマテリアルの Emission の値の有無とします。
Payload の拡張
パストレーシングを実装するに当たってレイトレシェーダ間でやりとりが必要なデータ(Payload)を加えます。
struct RayPayload
{
bool hit;
float3 radiance;
float3 emission;
float3 position;
float3 normal;
float4 randVal;
float3 reflect_direction;
float3 weight;
};
前々回から emission 以下を追加しています。
GPU レイトレにおいて Payload の大きさはパフォーマンスに大きく関わるそうです。
必要なデータの精度などによってはもっとコンパクトに実装できるかもしれませんが、今はわかりやすさ重視にしてあります。
パストレーシングループの実装
レンダリング方程式において入れ子になっている部分には、ループで実装するのか再帰で実装するのかという選択肢があります。
再帰は式通りに実装出来るのでわかりやすいですし、そのために TraceRay 関数は再帰できるようになっています。
しかし DXR には再帰の回数制限もありパフォーマンス的によいとは言えないため、今回はループで実装します。
パストレーシング本体を MyPathTracingShader.raytrace の Ray Generation シェーダ内に実装します。
もともと TraceRay するだけだけだった箇所がループに書き換わります。
最大の反射回数(ループ回数)は MAX_RAY_DEPTH として適当に定義します。
あまり大きすぎると PC スペックによっては重くなることに注意してください。
(10回は多すぎるかもしれません。)
#define MAX_RAY_DEPTH 10
同時に乱数を作る処理も入っています。
今はスクリーン座標(dispatchIdx)だけで初期化しています。
反射の度に乱数を4つ生成して Payload 経由で Closest Hit シェーダに渡しています。
(しばらくは1反射4つの乱数で十分な想定でいます。)
RayPayload payload = (RayPayload)0;
RNG rng;
rng.init(dispatchIdx, 0 /*frame count*/, 0 /* dimension */);
float3 radiance = 0;
float3 throughput = 1;
[unroll]
for(int i = 0; i < MAX_RAY_DEPTH; i++)
{
// この反射で使う乱数
payload.randVal = rng.rand();
// レイを飛ばす
TraceRay(_Scene, 0, 0xFF, 0, 1, 0, ray, payload);
// 直接光を評価
if (payload.hit)
{
radiance += throughput * payload.radiance;
}
// 空を評価
if (!payload.hit)
{
radiance += throughput * payload.radiance;
break;
}
// 発光を評価
if (any(payload.emission != 0))
{
radiance += throughput * payload.emission;
break;
}
// スループットを更新
throughput *= payload.weight;
// レイを更新
ray.Origin = payload.position + 1e-6 * payload.normal;
ray.Direction = payload.reflect_direction;
}
_Result[dispatchIdx] = float4(radiance, 1.0);
ここで重要なのは、レイの反射毎に加算していく放射輝度の radiance に加えて、throughput という値を使っている点です。
先ほど説明したとおり、今解きたいレンダリング方程式は反射が入れ子の形で表されます。
$$ L_0(\boldsymbol{x}_0, \boldsymbol{\omega}_0) = ({L_e}_0 + \frac{f(\boldsymbol{x}_0, \boldsymbol{\omega}_1, \boldsymbol{\omega}_0) | \boldsymbol{\omega}_0 \cdot \boldsymbol{n}_0 |}{p(\boldsymbol{\omega}_0)}) \left( \dots \left( {L_e}_N(\boldsymbol{x}_N, \boldsymbol{\omega}_N) \right) \right) $$
このパストレーシングは、カメラからレイを飛ばすので、数式的には内側の値を知らずに外側から評価していくことになります。
(カメラから反射の度に($x_0$ -> $x_1$ -> … -> $x_N$)と進んでいきます。)
反射の度に $\frac{f(\boldsymbol{x}_k, \boldsymbol{\omega}_{k+1}, \boldsymbol{\omega}_k) | \boldsymbol{\omega}_k \cdot \boldsymbol{n}_k |}{p(\boldsymbol{\omega}_k)}$ の部分は乗算されていき、最終的に色が確定するのは発光面(もしくは空)に当たった(一番最後の $L_e$ が決まった)ときです。
この乗算する値を反射毎に積み重ねていくのが throughput の役割です。radiance は反射ごとの $L_e$ (直接光、発光、空)を加算していきます(発光、空はそこで打ち切り)。
加算する際に、そこまでの反射で積み重なってきた throughput がかかります。
ちなみにこの値を throughput ではなく weight と呼ぶことも多いです。
今回は、パストレループの中で積み重なる値を throughput、個々の反射での値を weight という名前で実装しています。
BRDF とサンプリングの実装
次に MyPathTracerHitShader.hlsl の Closest Hit シェーダにパストレーシングに必要な情報の実装を追加します。
今必要な実装は主に payload.weight の計算です。
つまり式では $\frac{f(\boldsymbol{x}_k, \boldsymbol{\omega}_{k+1}, \boldsymbol{\omega}_k) | \boldsymbol{\omega}_k \cdot \boldsymbol{n}_k |}{p(\boldsymbol{\omega}_k)}$ の部分です。
ここまでレンダリング方程式の $f$ は BRDF とだけいってあまり説明していませんでした。
BRDF とは Bidirectional Reflectance Distribution Function の略で、日本語では双方向反射率分布関数と言います。
物体の反射特性を表す関数で、ある方向から光が入射したときに反射する光がどのように分布するのかを示します。
難しいですが物体の素材(マテリアル)を決めるための計算です。
なお反射だけを扱う場合は Reflectance の R ですが、透過を含めると Transmittance で BTDF、散乱を含めると Scattering で BSDF とも言います。
リアルタイムレンダリングでは透過と散乱を反射に統合して扱うことがないので BRDF とだけ言うことが多いです。
パストレーシングの文脈では全てを扱うので BSDF と言うことの方が多いかもしれません。
(どれかを示す意味で BxDF と書くこともあります。)
ランバートの拡散反射モデル
今回は BRDF に、有名な拡散反射モデルであるランバート反射を選びました。
光の反射には拡散反射と鏡面反射がありますが、鏡面反射を含んだ実装は少し複雑になるのでそちらはまた次回以降に解説できればと思います。
ランバート反射は昔から広く使われていて、 $\boldsymbol{n} \cdot \boldsymbol{\omega}_i$ のような法線と光の方向の内積に拡散反射の色をかけた式で表されます。
この内積はレンダリング方程式を見ると既に含まれています(コサイン項といいます)。
なのでパストレーシングの(というより PBR の文脈における)ランバート反射の BRDF は、コサイン項を除いて拡散反射率(つまり素材の色) $\rho$ を使って以下で表されます。
$$ f(\boldsymbol{x}, \boldsymbol{\omega}_i, \boldsymbol{\omega}_o) = \frac{\rho}{\pi}$$
分母の $\pi$ はエネルギー保存則を満たすための正規化項です。
この導出を行っている人も沢山いるので興味があれば調べてみてください。
ランバートの拡散反射モデルのサンプリング
次に考えるのは、反射方向 $\boldsymbol{\omega}_i$ をどうやって選ぶのか、ということです。
確率で反射方向を選ぶサンプリング処理を行います。
光は当たった点からその法線方向を中心にした半球方向のどこかへ必ず反射するはずです。
なので一様な Hemisphere (半球)サンプリングを行えば良いように思えますし、実際拡散反射はそれでことが足ります。
ただ愚直に半球上を一様にサンプリングするような処理には無駄があります。
パストレーシングでは反射特性(BRDF)に基づいて、光が強く反射する方向が確率的に選ばれやすくなるサンプリング戦略がよく使われています。
これは、パストレーシングの数値解法であるモンテカルロ積分を効率的に計算するための Importance Sampling (和訳は色々ありますが、重点的サンプリングが一般的でしょうか)という手法です。
ここで言う効率的とは数値計算の分散を低減するという意味で、パストレーシングにおいては少ないサンプルでよりノイズの少ない絵をつくることを示しています。
Importance Sampling についての詳しい説明は省略しますが、ランバート反射のサンプリングには Cosine-weighted hemisphere sampling (コサイン重み付き半球サンプリング)がよく使われています。
実装
ランバート反射の BRDF にしても Cosine-weighted hemisphere sampling にしても実装はそんなに複雑ではありません。
なので自分で実装しても良いのですが既に URP にも関数が用意されているのでそれを使います。
ImageBasedLighting.hlsl にそのための ImportanceSampleLambert 関数があるのでインクルードしておきます。
#include "Packages/com.unity.render-pipelines.core/ShaderLibrary/ImageBasedLighting.hlsl"
MyUniversalFragmentPBR を使って色だけを計算していた箇所を書き換えましょう。
if(any(surfaceData.emission != 0))
{
// 発光面(Le != 0)では直接光も評価しないで終了とする
payload.emission = surfaceData.emission;
payload.weight = 1;
payload.radiance = 0;
}
else
{
// 数値的なライトを評価
float3 directLighting = MyUniversalFragmentPBR(inputData, surfaceData).rgb;
payload.radiance = directLighting;
payload.emission = 0;
float nl, w;
// ImageBasedLighting.hlsl
ImportanceSampleLambert(payload.randVal.xy, inputData.tangentToWorld,
/*out*/ payload.reflect_direction, /*out*/ nl, /*out*/ w);
// 本当は BRDFData.diffuse を使うべきだが、今はベースカラーをそのまま拡散反射の色とする
payload.weight = surfaceData.albedo * w;
}
payload.hit = true;
payload.position = inputData.positionWS;
payload.normal = inputData.normalWS;
まず surfaceData からマテリアルの emission の値を取得し、非ゼロであれば発光面として payload.emission にデータを設定します。
この面以降の反射は行わないので BRDF は評価せず、radiance は 0、weight は 1 とします。
(発光の強さによっては以降の反射も行った方か正確な結果が得られると思います。)
発光面でないときは、MyUniversalFragmentPBR で直接光を計算して payload.radiance に設定します。
次の反射方向を決めるサンプリング処理を ImportanceSampleLambert 関数で行います。ImportanceSampleLambert 関数は、以下のように宣言されていて、2次元の乱数を入力に反射方向を計算してくれます。
// weightOverPdf return the weight (without the diffuseAlbedo term) over pdf. diffuseAlbedo term must be apply by the caller.
void ImportanceSampleLambert(real2 u,
real3x3 localToWorld,
out real3 L,
out real NdotL,
out real weightOverPdf)
得られた反射方向 L はそのまま payload.reflect_direction に設定します。
同時に得られる weightOverPdf はレンダリング方程式における $\frac{f(\boldsymbol{x}_k, \boldsymbol{\omega}_{k+1}, \boldsymbol{\omega}_k) | \boldsymbol{\omega}_k \cdot \boldsymbol{n}_k |}{p(\boldsymbol{\omega}_k)}$ の部分が入ります。
BRDF とコサイン項を PDF で割ったウエイトの値です。
(色は含んでないので後で適用します。)
PDF(確率密度関数)については全く説明していませんが、この $p(\boldsymbol{\omega}_0)$ は一様でない確率分布を使ったサンプリング操作で正しく値を累積するために必要な項で Importance Sampling における重要な計算です。
実は Cosine-weighted hemisphere sampling の weightOverPdf は 1 になります。
興味がある方は検算してみてください。ImportanceSampleLambert のソースコードを見ると BRDF と PDF とコサイン項がうまく打ち消し合って 1 になるということがコメントで注釈されています。
最後に weightOverPdf に拡散反射の反射率(色)をかけて payload.weight に設定します。
URP 的には拡散反射の色は brdfData.diffuse に格納されているのですが、今は拡散反射だけを扱うようにしているので、surfaceData.albedo に格納されているベースカラーを使っています。
正しい拡散反射の色は鏡面反射を実装するとき改めて対応しましょう。
これでパストレーシングで絵が描けるようになりました。

メインライトの明るさに合わせて前々回から空の明るさを5倍にしています。

直接光無しにして、シーン中に発光するオブジェクトを置いてみました。
Temporal Accumulation(実装は次回以降)
現状の絵にはノイズが多いことが分かります。
これはレンダリング方程式を解くためのモンテカルロ積分のサンプル数(1ピクセルあたりのレイの本数)が少ないため、数値計算の分散(誤差)が大きくなっているからです。
サンプル数を増やすために TraceRay を何回も行うようなループを実装しても良いのですが、Temporal Accumulation という時間軸方向でサンプル数を増やす方法もよく使われています。
ここまでで長くなってしまったので実装の説明は次回以降に持ち越しますが、Temporal Accumulation を行うとよりきれいな絵が得られます。


それでもまだノイズがわかるのでより高度なデノイズ戦略が必要そうです。
今回の様なフルパストレーシングは対象外なのですが、私が CEDEC 2021 で行ったレイトレーシングのデノイズについての講演でデノイズの基本的な考え方を紹介しています。
気になる方は、こちらに公開されている「リアルタイムレイトレーシング時代を生き抜くためのデノイザー開発入門」の資料を確認してみてください。
まとめ
絵を出すまで結構長くなってしまいましたが、これで Unity6 の URP 上にシンプルなパストレーサーを構築できました。
鏡面反射、ノイズの改善、動作の軽量化、半透明など扱いたいテーマは色々あるので次回以降さらにパストレーサーの機能拡充を図っていきたいと思います。
ソースコード
今回作ったソースコードの全文を載せます。MyPathTracerLit.shader、Random.hlsl、Payload.hlsl、C# スクリプトは割愛します。
▼MyPathTracingShader.raytrace 全文
#include "Packages/com.unity.render-pipelines.core/ShaderLibrary/Common.hlsl"
#include "Packages/com.unity.render-pipelines.universal/ShaderLibrary/Core.hlsl"
#include "Packages/com.unity.render-pipelines.universal/ShaderLibrary/UnityInput.hlsl"
#include "Payload.hlsl"
#include "Random.hlsl"
#pragma max_recursion_depth 2
RaytracingAccelerationStructure _Scene;
RWTexture2D<float4> _Result;
// https://github.com/boksajak/referencePT/blob/master/shaders/PathTracer.hlsl
RayDesc generatePinholeCameraRay(float2 pixel)
{
float4x4 view = unity_WorldToCamera;
float4x4 proj = unity_CameraProjection;
// Setup the ray
RayDesc ray;
ray.Origin = _WorldSpaceCameraPos;
ray.TMin = T_MIN;
ray.TMax = T_MAX;
// Extract the aspect ratio and field of view from the projection matrix
float aspect = proj[1][1] / proj [0][0];
float tanHalfFovY = 1.0f / proj [1][1];
// Compute the ray direction for this pixel
ray.Direction = normalize(
(pixel.x * view[0].xyz * tanHalfFovY * aspect) -
(pixel.y * view[1].xyz * tanHalfFovY) + view[2].xyz);
return ray;
}
#define MAX_RAY_DEPTH 10
[shader("raygeneration")]
void MyRaygenShader()
{
uint2 dispatchIdx = DispatchRaysIndex().xy;
uint2 dispatchSize = DispatchRaysDimensions().xy;
// Create the ray descriptor for this pixel
float2 clipPixel = (dispatchIdx + 0.5) / (float2)dispatchSize;
clipPixel.y = 1.0 - clipPixel.y;
clipPixel = clipPixel * 2.0 - 1.0;
RayDesc ray = generatePinholeCameraRay(clipPixel);
RayPayload payload = (RayPayload)0;
RNG rng;
rng.init(dispatchIdx, /* sample index */ 0, /* dimension */ 0);
float3 radiance = 0;
float3 throughput = 1;
[unroll]
for(int i = 0; i < MAX_RAY_DEPTH; i++)
{
// この反射で使う乱数
payload.randVal = rng.rand();
// レイを飛ばす
TraceRay(_Scene, 0, 0xFF, 0, 1, 0, ray, payload);
// 直接光を評価
if (payload.hit)
{
radiance += throughput * payload.radiance;
}
// 空を評価
if (!payload.hit)
{
radiance += throughput * payload.radiance;
break;
}
// 発光を評価
if (any(payload.emission != 0))
{
radiance += throughput * payload.emission;
break;
}
// スループットを更新
throughput *= payload.weight;
// レイを更新
ray.Origin = payload.position + 1e-6 * payload.normal;
ray.Direction = payload.reflect_direction;
}
_Result[dispatchIdx] = float4(radiance, 1.0);
}
[shader("miss")]
void MyMissShader(inout RayPayload payload : SV_RayPayload)
{
float t = WorldRayDirection().y * 0.9 + 0.1;
t = saturate(pow(t, 0.2));
payload.radiance = lerp(float3(0.5, 0.5, 0.7), float3(0.1, 0.3, 0.8), t) * 5;
payload.weight = 1;
payload.hit = false;
}
[shader("miss")]
void ShadowMissShader(inout ShadowPayload payload : SV_RayPayload)
{
payload.hit = false;
}
▼MyPathTracerHitShader.hlsl 全文
// 先に SAMPLE_TEXTURE2D を定義するインクルードをしておく
#include "Packages/com.unity.render-pipelines.universal/ShaderLibrary/Core.hlsl"
// 現状は RayTracing シェーダでミップマップは使えないので、
// SAMPLE_TEXTURE2D を使ったときに Mip0 に強制するように定義を置き換える
#ifdef SAMPLE_TEXTURE2D
#undef SAMPLE_TEXTURE2D
#define SAMPLE_TEXTURE2D(textureName, samplerName, coord) \
SAMPLE_TEXTURE2D_LOD(textureName, samplerName, coord, 0)
#endif
#include "Packages/com.unity.render-pipelines.core/ShaderLibrary/ImageBasedLighting.hlsl"
#include "Packages/com.unity.render-pipelines.universal/Shaders/LitInput.hlsl"
#include "Packages/com.unity.render-pipelines.universal/ShaderLibrary/Lighting.hlsl"
#include "Packages/com.unity.render-pipelines.universal/ShaderLibrary/ShaderGraphFunctions.hlsl"
#include "UnityRaytracingMeshUtils.cginc"
#include "Payload.hlsl"
#define M_PI 3.14159265
#define EPSILON 1e-12
RaytracingAccelerationStructure _Scene;
struct AttributeData
{
float2 barycentrics;
};
struct Vertex
{
float3 position;
float3 normal;
float4 tangent;
float2 texCoord0;
float2 texCoord1;
float2 texCoord2;
float2 texCoord3;
float4 color;
};
// Unity ビルトイン関数を使って頂点データを得る関数
Vertex FetchVertex(uint vertexIndex)
{
Vertex v;
v.position = UnityRayTracingFetchVertexAttribute3(vertexIndex, kVertexAttributePosition);
v.normal = UnityRayTracingFetchVertexAttribute3(vertexIndex, kVertexAttributeNormal);
v.tangent = UnityRayTracingFetchVertexAttribute4(vertexIndex, kVertexAttributeTangent);
v.texCoord0 = UnityRayTracingFetchVertexAttribute2(vertexIndex, kVertexAttributeTexCoord0);
v.texCoord1 = UnityRayTracingFetchVertexAttribute2(vertexIndex, kVertexAttributeTexCoord1);
v.texCoord2 = UnityRayTracingFetchVertexAttribute2(vertexIndex, kVertexAttributeTexCoord2);
v.texCoord3 = UnityRayTracingFetchVertexAttribute2(vertexIndex, kVertexAttributeTexCoord3);
v.color = UnityRayTracingFetchVertexAttribute4(vertexIndex, kVertexAttributeColor);
return v;
}
// レイトレのヒットした位置から頂点データを補間する関数
Vertex InterpolateVertices(Vertex v0, Vertex v1, Vertex v2, float3 barycentrics)
{
Vertex v;
#define INTERPOLATE_ATTRIBUTE(attr) v.attr = v0.attr * barycentrics.x + v1.attr * barycentrics.y + v2.attr * barycentrics.z
INTERPOLATE_ATTRIBUTE(position);
INTERPOLATE_ATTRIBUTE(normal);
INTERPOLATE_ATTRIBUTE(tangent);
INTERPOLATE_ATTRIBUTE(texCoord0);
INTERPOLATE_ATTRIBUTE(texCoord1);
INTERPOLATE_ATTRIBUTE(texCoord2);
INTERPOLATE_ATTRIBUTE(texCoord3);
INTERPOLATE_ATTRIBUTE(color);
return v;
}
// from : LitForwardPass.hlsl
void InitializeInputData(Vertex input, half3 normalTS, out InputData inputData)
{
inputData.positionWS = WorldRayOrigin() + RayTCurrent() * WorldRayDirection();
inputData.positionCS = 0;
inputData.viewDirectionWS = WorldRayDirection();
inputData.shadowCoord = 0;
inputData.fogCoord = 0;
inputData.vertexLighting = 0;
inputData.bakedGI = 0;
inputData.shadowMask = 0;
inputData.normalizedScreenSpaceUV = DispatchRaysIndex().xy / DispatchRaysDimensions().xy;
// レイトレ用の変換行列を使ってワールド法線と接線を解決する
float3 normalWS = normalize(mul(input.normal, (float3x3)WorldToObject3x4()));
// Tangent はあるものとして計算(レイトレではノーマルマップの計算以外にも必須)
float4 tangentWS = float4(normalize(mul(input.tangent.xyz, (float3x3)WorldToObject3x4())), input.tangent.w);
inputData.tangentToWorld = BuildTangentToWorld(tangentWS, normalWS); // ShaderGraphFuction.hlsl
#if defined(_NORMALMAP) || defined(_DETAIL)
inputData.normalWS = TransformTangentToWorld(normalTS, inputData.tangentToWorld); // SpaceTransforms.hlsl
#else
inputData.normalWS = normalWS;
#endif
// inputData は Shadow/GI 関係のデータも扱うが、今回はそれらはレイトレで解決するので用意しない
}
float TraceShadow(float3 lightDirection, float3 normalWS, float3 positionWS)
{
RayDesc ray;
ray.Origin = positionWS + 1e-6 * normalWS;
ray.Direction = lightDirection;
// シーンスケールに合わせて適切に設定すべき
ray.TMin = 0.1;
ray.TMax = 100;
ShadowPayload payload = (ShadowPayload)0;
payload.hit = true;
TraceRay(_Scene, RAY_FLAG_SKIP_CLOSEST_HIT_SHADER | RAY_FLAG_ACCEPT_FIRST_HIT_AND_END_SEARCH,
0xFF, 0, 1, 1 /* ShadowMissShader */, ray, payload);
return (float)!payload.hit;
}
// from : Lighting.hlsl
half4 MyUniversalFragmentPBR(InputData inputData, SurfaceData surfaceData)
{
#if defined(_SPECULARHIGHLIGHTS_OFF)
bool specularHighlightsOff = true;
#else
bool specularHighlightsOff = false;
#endif
BRDFData brdfData;
// NOTE: can modify "surfaceData"...
InitializeBRDFData(surfaceData, brdfData);
// Clear-coat calculation...
BRDFData brdfDataClearCoat = CreateClearCoatBRDFData(surfaceData, brdfData);
uint meshRenderingLayers = GetMeshRenderingLayer();
Light mainLight = GetMainLight();
mainLight.shadowAttenuation = TraceShadow(mainLight.direction, inputData.normalWS, inputData.positionWS);
LightingData lightingData = CreateLightingData(inputData, surfaceData);
lightingData.giColor = 0; // GI はパストレで解決する
#ifdef _LIGHT_LAYERS
if (IsMatchingLightLayer(mainLight.layerMask, meshRenderingLayers))
#endif
{
lightingData.mainLightColor = LightingPhysicallyBased(brdfData, brdfDataClearCoat,
mainLight,
inputData.normalWS, inputData.viewDirectionWS,
surfaceData.clearCoatMask, specularHighlightsOff);
}
#if defined(_ADDITIONAL_LIGHTS)
uint pixelLightCount = GetAdditionalLightsCount();
#if USE_FORWARD_PLUS
[loop] for (uint lightIndex = 0; lightIndex < min(URP_FP_DIRECTIONAL_LIGHTS_COUNT, MAX_VISIBLE_LIGHTS); lightIndex++)
{
FORWARD_PLUS_SUBTRACTIVE_LIGHT_CHECK
Light light = GetAdditionalLight(lightIndex, inputData.positionWS);
//light.shadowAttenuation = TraceShadow(light.direction, inputData.normalWS, inputData.positionWS);
#ifdef _LIGHT_LAYERS
if (IsMatchingLightLayer(light.layerMask, meshRenderingLayers))
#endif
{
lightingData.additionalLightsColor += LightingPhysicallyBased(brdfData, brdfDataClearCoat, light,
inputData.normalWS, inputData.viewDirectionWS,
surfaceData.clearCoatMask, specularHighlightsOff);
}
}
#endif // USE_FORWARD_PLUS
LIGHT_LOOP_BEGIN(pixelLightCount)
Light light = GetAdditionalLight(lightIndex, inputData.positionWS);
//light.shadowAttenuation = TraceShadow(light.direction, inputData.normalWS, inputData.positionWS);
#ifdef _LIGHT_LAYERS
if (IsMatchingLightLayer(light.layerMask, meshRenderingLayers))
#endif
{
lightingData.additionalLightsColor += LightingPhysicallyBased(brdfData, brdfDataClearCoat, light,
inputData.normalWS, inputData.viewDirectionWS,
surfaceData.clearCoatMask, specularHighlightsOff);
}
LIGHT_LOOP_END
#endif // _ADDITIONAL_LIGHTS
#if REAL_IS_HALF
// Clamp any half.inf+ to HALF_MAX
return min(CalculateFinalColor(lightingData, surfaceData.alpha), HALF_MAX);
#else
return CalculateFinalColor(lightingData, surfaceData.alpha);
#endif
}
[shader("closesthit")]
void ClosestHitMain(inout RayPayload payload : SV_RayPayload, AttributeData attribs : SV_IntersectionAttributes)
{
// レイトレのヒットした位置から頂点インデックスを取得
uint3 triangleIndices = UnityRayTracingFetchTriangleIndices(PrimitiveIndex());
// 頂点インデックスから三角形の3頂点を取得
Vertex v0, v1, v2;
v0 = FetchVertex(triangleIndices.x);
v1 = FetchVertex(triangleIndices.y);
v2 = FetchVertex(triangleIndices.z);
// 3頂点からをヒット位置で補間
float3 barycentricCoords = float3(1.0 - attribs.barycentrics.x - attribs.barycentrics.y, attribs.barycentrics.x, attribs.barycentrics.y);
Vertex v = InterpolateVertices(v0, v1, v2, barycentricCoords);
// テクスチャ座標の変形(元は LitPassVertex の処理)
v.texCoord0 = TRANSFORM_TEX(v.texCoord0, _BaseMap);
SurfaceData surfaceData;
InitializeStandardLitSurfaceData(v.texCoord0, surfaceData);
InputData inputData;
InitializeInputData(v, surfaceData.normalTS, inputData);
if(any(surfaceData.emission != 0))
{
// 発光面(Le != 0)では直接光も評価しないで終了とする
payload.emission = surfaceData.emission;
payload.weight = 1;
payload.radiance = 0;
}
else
{
// 数値的なライトを評価
float3 directLighting = MyUniversalFragmentPBR(inputData, surfaceData).rgb;
payload.radiance = directLighting;
payload.emission = 0;
float nl, w;
// ImageBasedLighting.hlsl
ImportanceSampleLambert(payload.randVal.xy, inputData.tangentToWorld,
/*out*/ payload.reflect_direction, /*out*/ nl, /*out*/ w);
// 本当は BRDFData.diffuse を使うべきだが、今はベースカラーをそのまま拡散反射の色とする
payload.weight = surfaceData.albedo * w;
}
payload.hit = true;
payload.position = inputData.positionWS;
payload.normal = inputData.normalWS;
}



